Dreizehneck

Das Dreizehneck oder Tridekagon (von altgriechisch τριςκαίδεκα triskaídeka, deutsch ‚dreizehn‘ und γωνία gōnía, deutsch ‚Winkel, Ecke‘)^[1] ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch dreizehn Punkte und deren dreizehn Verbindungen, bezeichnet als Strecken, Seiten oder Kanten.

Das Dreizehneck ist darstellbar als:

• konkaves Dreizehneck, in dem mindestens ein Innenwinkel größer als 180° ist. Ein Dreizehneck kann höchstens sechs solche Winkel haben.
• konvexes Dreizehneck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Dreizehneck kann regelmäßig oder unregelmäßig sein.
• Sehnendreizehneck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen ungleich sind.
• regelmäßiges Dreizehneck: Es ist bestimmt durch dreizehn Punkte auf einem virtuellen Kreis. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Strecken, auch Seiten oder Kanten genannt, verbunden.
• regelmäßiges überschlagenes Dreizehneck: Es ergibt sich, wenn beim Verbinden der dreizehn Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

In der folgenden Galerie sind die fünf möglichen regelmäßigen Dreizehnstrahlsterne, auch Tridekagramme genannt, dargestellt.

• Regelmäßige Dreizehnstrahlsterne
• 
  ${\displaystyle \left\{13/2\right\}{,}\ \left\{13/11\right\}}$
• 
  ${\displaystyle \left\{13/3\right\}{,}\ \left\{13/10\right\}}$
• 
  ${\displaystyle \left\{13/4\right\}{,}\ \left\{13/9\right\}}$
• 
  ${\displaystyle \left\{13/5\right\}{,}\ \left\{13/8\right\}}$
• 
  ${\displaystyle \left\{13/6\right\}{,}\ \left\{13/7\right\}}$

Das regelmäßige Dreizehneck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel kein konstruierbares Polygon, denn seine Seitenanzahl ${\displaystyle n=13}$ ist kein Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen.

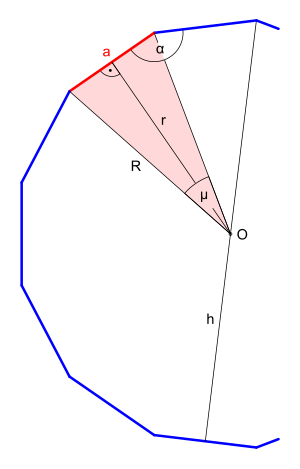
Größen eines regelmäßigen Dreizehnecks
Innenwinkel	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {11}{13}}\cdot 180^{\circ }\\\alpha &=152{,}{\overline {307692}}^{\circ }\end{aligned}}}$
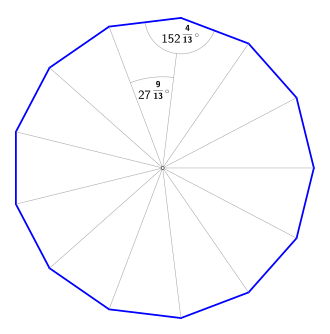
Zentriwinkel (Mittelpunktswinkel)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{13}}\\\mu &=27{,}{\overline {692307}}^{\circ }\end{aligned}}}$
Seitenlänge	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\\a&=R\cdot \left[{\frac {1}{6}}{\sqrt {26+6{\sqrt {13}}}}-{\frac {1}{3}}{\sqrt {26-6{\sqrt {13}}}}\cos \left[{\frac {1}{3}}\arctan \left({\frac {3{\sqrt {3}}}{5}}\right)\right]\right]\\a&\approx 0{,}478631\cdot R\end{aligned}}}$
Umkreisradius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}}\\R&\approx {\frac {a}{0{,}478631}}\end{aligned}}}$
Inkreisradius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\r&=R\cdot \left[{\frac {{\sqrt {13}}+3}{8}}+{\frac {{\sqrt {13}}-1}{8{\sqrt {3}}}}\tan \left[{\frac {\pi }{6}}+{\frac {1}{6}}\arctan \left({\frac {3{\sqrt {3}}}{5}}\right)\right]\right]\\r&\approx 0{,}970941\cdot R\end{aligned}}}$
Höhe	${\displaystyle {\begin{aligned}h&=R+r=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{13}}\right)\right)\\h&\approx 1{,}9709418\cdot R\end{aligned}}}$
Flächeninhalt	${\displaystyle {\begin{aligned}A&=13\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\A&\approx 3{,}0207006\cdot R^{2}\end{aligned}}}$

Der Innenwinkel ${\displaystyle \alpha }$ wird von zwei benachbarten Seitenkanten eingeschlossen. In der allgemeinen Formel für regelmäßige Polygone steht die Variable ${\displaystyle n}$ für die Anzahl der Eckpunkte des Polygons. In diesem Fall ist für die Variable die Zahl ${\displaystyle 13}$ einzusetzen.

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {13-2}{13}}\cdot 180^{\circ }={\frac {11}{13}}\cdot 180^{\circ }=152{,}{\overline {307692}}^{\circ }}$

Der Zentriwinkel oder Mittelpunktswinkel ${\displaystyle \mu }$ wird von zwei benachbarten Umkreisradien ${\displaystyle R}$ eingeschlossen. In der allgemeinen Formel ist für die Variable ${\displaystyle n}$ die Zahl ${\displaystyle 13}$ einzusetzen.

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{13}}=27{,}{\overline {692307}}^{\circ }}$

Das Dreizehneck ist in dreizehn gleichschenklige Dreiecke, sogenannte Teildreiecke, teilbar. Aus der Hälfte eines solchen Teildreiecks, sprich aus einem rechtwinkligen Dreieck mit der Kathete (halbe Seitenlänge) ${\displaystyle {\frac {a}{2}}}$, der Hypotenuse (Umkreisradius) ${\displaystyle R}$ und dem halben Zentriwinkel ${\displaystyle {\frac {\mu }{2}}}$ erhält man mithilfe der Trigonometrie im rechtwinkligen Dreieck die Seitenlänge ${\displaystyle a}$ wie folgt

${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {\mu }{2}}\right)=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\\&=R\cdot 2\cdot \sin \left(13{,}{\overline {846153}}^{\circ }\right)\\a&\approx 0{,}478631\cdot R,\end{aligned}}}$

durch Umformen erhält man den Umkreisradius ${\displaystyle R}$

${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}}\\R&\approx {\frac {a}{0{,}478631}}\end{aligned}}}$

Der Inkreisradius ${\displaystyle r}$ ist die Höhe eines Teildreiecks, senkrecht zur Seitenlänge ${\displaystyle a}$ des Dreizehnecks. Wird zur Berechnung wieder das gleiche rechtwinklige Dreieck wie bei der Seitenlänge verwendet, gilt für den Inkreisradius ${\displaystyle r}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\r&\approx 0{,}970941\cdot R\end{aligned}}}$

Die Höhe ${\displaystyle h}$ eines regelmäßigen Dreizehneckes ergibt sich aus der Summe von Inkreisradius und Umkreisradius.

${\displaystyle h=R+r=R+R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{13}}\right)\right)}$

${\displaystyle h\approx 1{,}970941817\cdot R}$

Der Flächeninhalt eines Dreiecks berechnet sich allgemein ${\displaystyle A_{\Delta }={\frac {1}{2}}a\cdot h_{a}}$. Für die Berechnung des Dreizehnecks werden die Ergebnisse der Seitenlänge ${\displaystyle a}$ und des Inkreisradius ${\displaystyle r}$ herangezogen, worin ${\displaystyle r}$ für die Höhe ${\displaystyle h_{a}}$ eingesetzt wird.

${\displaystyle a=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle h_{a}=r=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\;}$ daraus folgt für die Fläche eines Teildreiecks

${\displaystyle {\begin{aligned}A_{\Delta }&={\frac {1}{2}}\cdot R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\end{aligned}}\;}$ zusammengefasst ergibt sich

${\displaystyle A_{\Delta }=R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle A_{\Delta }\approx 0{,}232361586\cdot R^{2}}$

und für die Fläche des gesamten Dreizehnecks

${\displaystyle A=13\cdot A_{\Delta }=13\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle A\approx 3{,}020700618\cdot R^{2}}$

Wie unter Regelmäßiges Dreizehneck begründet, ergibt eine Konstruktion mit Zirkel und Lineal keine Lösung. Gelten jedoch zusätzliche Hilfsmittel, wie z. B. die Methode des Archimedes, Bieberbachs Rechtwinkelhaken und der Tomahawk für eine Dreiteilung des Winkels oder die Kurven Quadratrix des Hippias und archimedische Spirale um den 90-Grad-Winkel in ${\displaystyle n}$ gleich große Winkel zu unterteilen, ist eine exakte Konstruktion machbar.

Andrew M. Gleason veröffentlichte 1988 in der mathematischen Zeitschrift The American Mathematical Monthly zwei elegante Konstruktionen zu den regelmäßigen Polygonen Siebeneck und Dreizehneck.^[2] Beide verlangen für eine exakte Lösung die Dreiteilung des Winkels. Die Methode hierfür ließ Andrew M. Gleason offen. Die folgende Konstruktionsskizze (linkes Bild des Doppelbildes) unterscheidet sich vom Original durch die Weiterführung der Konstruktion bis zum fertigen Dreizehneck. Die gepunkteten Linien dienen der Verdeutlichung, z. B. wie man bestimmte Funktionspunkte erzeugt. Näheres hierzu in der nachfolgenden Beschreibung anhand der Originalbeschreibung.

Dreizehneck, Konstruktionsskizze mit Tomahawk (hellblau)

Animation der Konstruktionsskizze

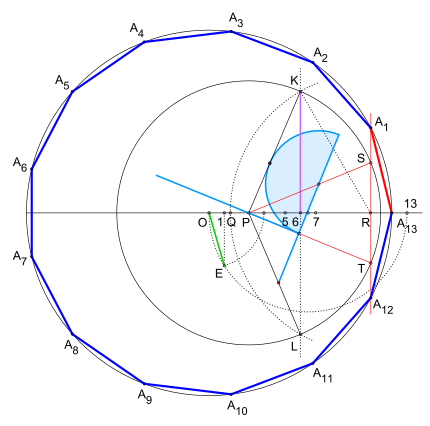
Für das Dreizehneck beginnt man im Koordinatenursprung eines kartesischen Koordinatensystems mit einem Kreis um Punkt ${\displaystyle O(0,0)}$ mit Radius ${\displaystyle 12}$. Es folgt die Festlegung des Punktes ${\displaystyle A_{13}(12,0)}$. Um den Punkt ${\displaystyle P\left({\sqrt {13}}-1,0\right)}$ zu erhalten, werden zunächst die Zahlenwerte ${\displaystyle 1}$, als zwölfter Teil von ${\displaystyle {\overline {O13}}}$, sowie ${\displaystyle 13}$ bestimmt, die Strecke ${\displaystyle {\overline {O13}}}$ halbiert und um deren Mittelpunkt der Thaleskreis gezogen. Die danach errichtete Senkrechte auf ${\displaystyle {\overline {O13}}}$ ab ${\displaystyle 1}$ schneidet den Thaleskreis in ${\displaystyle E}$. Die Verbindung des Punktes ${\displaystyle O}$ mit ${\displaystyle E}$ ergibt ${\displaystyle {\sqrt {13}}}$ für das Eintragen des Punktes ${\displaystyle P\left({\sqrt {13}}-1,0\right)}$. Im Anschluss die Zahlenwerte ${\displaystyle 5}$ und ${\displaystyle 7}$ auf ${\displaystyle {\overline {O13}}}$ ermitteln sowie die Punkte ${\displaystyle Q\left(5-{\sqrt {13}},0\right)}$ und ${\displaystyle R\left(7+{\sqrt {13}},0\right)}$ einzeichnen.

Zum Finden der Punkte ${\displaystyle K}$ und ${\displaystyle L}$ wird zuerst der Zahlenwert ${\displaystyle 6}$ auf ${\displaystyle {\overline {O13}}}$ festgelegt und eine Senkrechte durch die ${\displaystyle 6}$ errichtet. Zieht man nun einen Kreisbogen um ${\displaystyle R}$ durch ${\displaystyle Q}$, schneidet er die Senkrechte in ${\displaystyle K\left(6,{\sqrt {3}}\cdot \left({\sqrt {13}}+1\right)\right)}$ und ${\displaystyle L\left(6,-{\sqrt {3}}\cdot \left({\sqrt {13}}+1\right)\right)}$. Nach dem Verbinden der Punkte ${\displaystyle K}$ und ${\displaystyle L}$ mit ${\displaystyle P}$ sowie dem Ziehen eines Kreises um ${\displaystyle P}$ durch ${\displaystyle K}$, wird der Winkel ${\displaystyle LPK}$ mit einer frei wählbaren Methode gedrittelt. Hier z. B. geschieht dies mithilfe eines sogenannten Tomahawks, dabei ergeben sich die Punkte ${\displaystyle S}$ und ${\displaystyle T}$. Eine Gerade durch ${\displaystyle S}$ und ${\displaystyle T}$ ergibt ${\displaystyle A_{1}}$ und ${\displaystyle A_{12}}$, die Eckpunkte eines regelmäßigen Dreizehnecks ${\displaystyle A_{1},\dots ,A_{13}}$ sind. Die übrigen Eckpunkte können durch Verwendung des Kreisbogens ${\displaystyle OA_{13}A_{1}}$ nacheinander gefunden werden.

Die Konstruktion (Bild 1) des Dreizehnecks mit vorgegebenem Umkreis ist nahezu gleich der des Elfecks. Aus diesem Grund wurde die Beschreibung des Elfecks mit den erforderlichen Anpassungen übernommen.

Nach dem Zeichen des Quadrates, z. B. mit der Seitenlänge ${\displaystyle 1}$, und des Umkreises um den Punkt ${\displaystyle O}$ durch ${\displaystyle A_{1}}$ erfolgt die Konstruktion der speziellen Kurve, der sogenannten Quadratrix des Hippias, mit der Parameterdarstellung ${\displaystyle \gamma \colon (0,{\tfrac {\pi }{2}})\rightarrow \mathbb {R} ^{2}}$:^[3][4]

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}}$

mit

${\displaystyle {\begin{aligned}x(t)&={\begin{cases}t\cot \left({\frac {\pi t}{2\cdot 1}}\right)\,&,0\leq t\leq 1\end{cases}}\\y(t)&=t\end{aligned}}}$

Danach wird die Strecke ${\displaystyle {\overline {CO}}}$ in dreizehn gleich lange Abschnitte mithilfe der Streckenteilung geteilt. Aus Gründen der Übersichtlichkeit sind in der Zeichnung nur die relevanten Punkte dargestellt.

Der Zentriwinkels des Dreizehnecks ergibt sich aus ${\displaystyle \mu ={\frac {360^{\circ }}{13}},}$ aber die Quadratrix des Hippias unterteilt nur die Winkel ab ${\displaystyle >0^{\circ }}$ bis ${\displaystyle \leq 90^{\circ }}$ in gleich große Winkel. Daraus folgt, ein Dreizehntel der Strecke ${\displaystyle {\overline {CO}}}$ kann nur ein Dreizehntel des Winkels ${\displaystyle 90^{\circ }}$ erzielen. Deshalb wird wegen der Berechnung des Zentriwinkels ${\displaystyle \mu }$ aus dem Umkreis mit seinen ${\displaystyle 360^{\circ },}$ das Vierfache eines Dreizehntels, d. h. der Teilungspunkt ${\displaystyle 4'}$ der Strecke ${\displaystyle {\overline {CO}},}$ zur Konstruktion des Zentriwinkels ${\displaystyle \mu }$ genutzt. Dieser entsteht nach der Konstruktion einer Parallelen zu ${\displaystyle {\overline {A_{1}O}}}$ ab ${\displaystyle 4'}$ bis zur Kurve der Quadratrix, dabei ergibt sich der Punkt ${\displaystyle D}$. Nun zieht man eine Halbgerade ab dem Winkelscheitel ${\displaystyle O}$ durch ${\displaystyle D}$ bis zum Umkreis. Somit ergibt sich auf dem Umkreis der zweite Eckpunkt ${\displaystyle A_{2}}$. Die Länge der Strecke ${\displaystyle {\overline {A_{1}A_{2}}}}$ ist die exakte Seitenlänge ${\displaystyle a}$ des regelmäßigen Dreizehnecks.

Nach dem elfmaligen Abtragen der Seitenlänge ${\displaystyle a}$ auf dem Umkreis gegen den Uhrzeigersinn und dem abschließenden Verbinden der benachbarten Eckpunkte, ist das Dreizehneck ${\displaystyle A_{1}\ldots A_{13}}$ fertiggestellt.

Die Konstruktion des Dreizehnecks mit vorgegebener Seitenlänge (siehe Bild 2) ist nahezu gleich der des Elfecks. Aus diesem Grund wurde die Beschreibung des Elfecks mit den erforderlichen Anpassungen übernommen.

Ist die Seitenlänge ${\displaystyle a'}$ eines Dreizehnecks mit vorgegebenem Umkreis bereits – exakt mithilfe der Quadratrix oder näherungsweise – bestimmt, kann daraus mithilfe der sogenannten zentrischen Streckung ein Dreizehneck mit vorgegebener Seitenlänge ${\displaystyle a}$ konstruiert werden.

Nur falls die vorgegebene Seitenlänge ${\displaystyle a}$ länger als ${\displaystyle a'}$ ist, werden zuerst beide Winkelschenkel des Zentriwinkels ${\displaystyle \mu }$ verlängert. Als Nächstes wird die Winkelhalbierenden ${\displaystyle wh}$ des Winkels ${\displaystyle \mu }$ eingezeichnet und anschließend darauf der Punkt ${\displaystyle M}$ mit beliebiger Position bestimmt. Es folgt eine Parallele zu ${\displaystyle a'={\overline {A_{1}'A_{2}'}}}$ durch ${\displaystyle M}$. Beim Ziehen des Halbkreises um ${\displaystyle M}$ mit Radius ${\displaystyle r={\frac {a}{2}}}$ ergeben sich die Schnittpunkte ${\displaystyle E}$ und ${\displaystyle F}$. Die beiden Parallelen zu ${\displaystyle wh}$ ab ${\displaystyle E}$ bzw. ${\displaystyle F}$, bis zu den betreffenden Winkelschenkeln, liefern die beiden ersten Eckpunkte ${\displaystyle A_{1}}$ und ${\displaystyle A_{2}}$ des gesuchten Dreizehnecks. Abschließend wird der somit gefundene Umkreis mit dem Radius ${\displaystyle r_{u}={\overline {OA_{1}}}}$ um ${\displaystyle O}$ gezogen, ab dem Eckpunkt ${\displaystyle A_{2}}$ die Seitenlänge ${\displaystyle a}$ elfmal gegen den Uhrzeigersinn auf dem Umkreis abgetragen und die benachbarten Eckpunkte miteinander verbunden.

Es sind nur wenige Näherungskonstruktionen des Dreizehnecks in der einschlägigen Literatur beschrieben.

Im Jahr 1525 veröffentlichte Albrecht Dürer in seinem Werk Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen im zweiten Buch ein Elfeck und ein Dreizehneck (im Bild 3 rechts).^[5] Das in einem Kreis einbeschriebene regelmäßige Dreizehneck, benötigt zum Bestimmen der Seitenlänge nur den halben Radius und den Punkt ${\displaystyle c}$, nahe dem Punkt ${\displaystyle b}$. Der Punkt ${\displaystyle c}$, Dürer hat ihn nicht näher erläutert, wird mithilfe von Versuchen (empirisch) festgelegt.

Dürer weist in seiner Beschreibung insbesondere darauf hin, dass dies eine näherungsweise („mechanische“) und keine exakte („demonstrative“) Konstruktion sei. Der absolute Fehler der so konstruierten ersten Seitenlänge ist abhängig von der Genauigkeit des empirisch ermittelten Punktes ${\displaystyle c}$.

Bild 4 zeigt ein Dreizehneck in seinem Umkreis, erstellt mit einer universellen Methode.^[6][7]

Zuerst wird die Strecke ${\displaystyle {\overline {AB}}}$, später der Durchmesser des gesuchten Dreizehnecks, in ${\displaystyle 13}$ gleich lange Teile mithilfe des Strahlensatzes geteilt (in der Zeichnung nicht dargestellt) oder mittels Aneinanderreihen von ${\displaystyle 13}$ gleich langen Abständen bestimmt. Nun werden entweder die geraden oder die ungeraden Zahlen (Teilungspunkte) auf ${\displaystyle {\overline {AB}}}$ markiert. In diesem Beispiel sind die geraden Zahlen ${\displaystyle 2,4,6,8,10}$ und ${\displaystyle 12}$ eingetragen. Die anschließende Halbierung von ${\displaystyle {\overline {AB}}}$ erfolgt mithilfe der zwei Kreisbögen um ${\displaystyle A}$ bzw. ${\displaystyle B}$ mit dem Radius ${\displaystyle {\overline {AB}}}$. Die Kreisbögen schneiden sich in den Punkten ${\displaystyle C}$ und ${\displaystyle D.}$ Durch deren Verbindung erhält man den Mittelpunkt ${\displaystyle O}$ und die Symmetrieachse.

Nach dem Einzeichnen des Umkreises um ${\displaystyle O}$ durch ${\displaystyle A}$ geht es weiter mit dem Festlegen der Eckpunkte auf dem Umkreis. Das Lineal wird an den Punkt ${\displaystyle D}$ und an die gerade Zahl ${\displaystyle 2}$ gelegt. Danach am Lineal entlang eine kurze Linie durch die gegenüberliegende Hälfte der Umkreislinie gezogen, ergibt den Eckpunkt ${\displaystyle E_{6}}$ des entstehenden Dreizehnecks. Diese Vorgehensweise wiederholt sich beim Bestimmen der Eckpunkte ${\displaystyle E_{5}\ldots E_{1}.}$ Sie wird fortgesetzt, jetzt ausgehend vom Punkt ${\displaystyle C,}$ bis die restlichen Eckpunkte ${\displaystyle E_{8}\ldots E_{13}}$ gefunden sind. Abschließend werden die benachbarten Eckpunkte miteinander verbunden.

Das Besondere an dieser Methode ist, sechs Seiten des Dreizehnecks haben paarweise die gleiche Länge, z. B. die Seiten ${\displaystyle {\overline {E_{6}E_{7}}}}$ und ${\displaystyle {\overline {E_{7}E_{8}}}.}$ Die Seite ${\displaystyle {\overline {E_{1}E_{13}}}}$ hat eine von den anderen unterschiedliche Länge.

Größter und kleinster absoluter Fehler der Seitenlängen bei einem Umkreisradius mit ${\displaystyle R=1\;\mathrm {m} }$:

${\displaystyle {\overline {E_{1}E_{13}}}\approx 21{,}26\;\mathrm {mm} }$

${\displaystyle {\overline {E_{4}E_{5}}}}$ und ${\displaystyle {\overline {E_{9}E_{10}}}\approx -1{,}176704\;\mathrm {mm} }$

${\displaystyle {\overline {E_{3}E_{4}}}}$ und ${\displaystyle {\overline {E_{10}E_{11}}}\approx 1{,}193636\;\mathrm {mm} }$

Sieht man sich die beiden kleinsten absoluten Fehler der benachbarten Seiten an, folgt daraus, beide sind nahezu gleich von einer idealen Mitte ${\displaystyle 0\;\mathrm {mm} }$ entfernt. Das bedeutet, würde man in dieser Näherungskonstruktion z. B. nur die Strecken ${\displaystyle {\overline {E_{9}E_{10}}}}$ und ${\displaystyle {\overline {E_{10}E_{11}}}}$ konstruieren, anschließend das arithmetische Mittel dieser Strecken konstruktiv ermitteln, ergäbe dies eine Seitenlänge des Dreizehnecks mit einer Abweichung von

${\displaystyle {\frac {1}{2}}\cdot \left(-1{,}176704\ldots \,\mathrm {mm} +1{,}193636\ldots \,\mathrm {mm} \right)=0{,}008466\ldots \;\mathrm {mm} }$.

Oder anders gesagt, bei einem Umkreisradius ${\displaystyle R=1\;\mathrm {km} }$ wäre die Abweichung der konstruierten ersten Seite ${\displaystyle \approx 8{,}5\;\mathrm {mm} }$.

• Beispiele zu Münzen mit der Form bzw. eingeprägten Figur eines regelmäßigen Dreizehnecks:

• 
  Tschechische 20-Kronen-Münze,
  mit gerundeten Kanten (1997)
  links Vorderseite mit dem Böhmischen Löwen,
  rechts Rückseite mit der Wenzelsstatue am Wenzelsplatz.
• 
  Tunesische 200-Millim-Münze (2013),
  mit gerundeten Kanten,
  links Rückseite, rechts Vorderseite.
• 
  Tunesische 2-Dinar-Münze (2013),
  mit gerundeten Kanten,
  links Rückseite mit dem Hafen von Karthago, rechts Vorderseite mit einem Olivenbaum.

• H. Maser: Die Teilung des Kreises ..., Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.

Wiktionary: Dreizehneck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Dreizehneck, Variante der Näherungskonstruktion mit einer universellen Methode
• Dreizehneck bei gegebener Seitenlänge ${\displaystyle a}$, exakte Konstruktion

1. ↑ Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 2. Juli 2024]). 
2. ↑ Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 193, JSTOR:2323624 (Online [PDF; 303 kB; abgerufen am 17. August 2021]). 
3. ↑ Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner 2003, S. 45–48 Die Quadratur des Kreises (Auszug (Google)), abgerufen am 29. Oktober 2017
4. ↑ Horst Hischer: Mathematik in der Schule 32 (1994) 5, Geschichte der Mathematik als didaktischer Aspekt (2). Lösung klassischer Probleme. (PDF; 2,1 MB) S. 279 ff., abgerufen am 29. Oktober 2017. 
5. ↑ Albrecht Dürer: Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen. Nürnberg 1525 (ETH-Bibliothek, Konstruktion eines regelmäßigen Elf- und Dreizehnecks, S. 63, Fig 19 [abgerufen am 17. Oktober 2017]). 
6. ↑ H. August: Zeichnerische Konstruktion eines Elfecks. In: Zeichnerische Konstruktionen: Mehrecke. Abgerufen am 17. Oktober 2017. 
7. ↑ Peter Eckardt: Siebeneck. In: Sterne und Polygone. Abgerufen am 17. Oktober 2017.