Minor (Graphentheorie)

In der Graphentheorie sind Minoren gewisse Graphen, die sich durch Kantenkontraktion und durch Weglassen von Kanten oder Knoten aus einem anderen Graphen gewinnen lassen. Die Minorenrelation ist neben der Teilgraphenrelation und der Unterteilungsrelation eine der wichtigsten Relationen der Graphentheorie und erlaubt viele tiefgehende Sätze wie z. B. den Satz von Kuratowski oder das Minorentheorem von Robertson und Seymour.

Alle genannten Graphen seien stets als einfach angenommen.

Ersetzt man die Knoten ${\displaystyle x\in V}$ eines Graphen ${\displaystyle G}$ durch disjunkte zusammenhängende Graphen ${\displaystyle G_{x}}$ sowie Kanten ${\displaystyle xy}$ durch ${\displaystyle G_{x}}$-${\displaystyle G_{y}}$-Kanten, so erhält man einen neuen Graphen, der ${\displaystyle IG}$ genannt wird (${\displaystyle I}$ für inflated). Diese Benennung leitet sich daraus her, dass durch die Ersetzung der Knoten durch Graphen der ursprüngliche Graph größer wird. Enthält nun ein Graph ${\displaystyle Z}$ ein ${\displaystyle IG}$, so nennt man ${\displaystyle G}$ einen Minor von ${\displaystyle Z}$.

Ist ${\displaystyle G}$ ein Graph, so heißt ein Graph ${\displaystyle TG}$ Unterteilungsgraph von ${\displaystyle G}$, falls er durch Unterteilung von Kanten aus ${\displaystyle G}$ hervorgegangen ist. Die Knoten von ${\displaystyle TG}$, die auch in ${\displaystyle G}$ enthalten sind, werden dann Verzweigungsknoten genannt, alle anderen Knoten heißen Unterteilungsknoten. Verzweigungsknoten erben ihren Grad aus ${\displaystyle G}$, Unterteilungsknoten sind alle vom Grad 2. Enthält ein Graph ${\displaystyle Z}$ einen Unterteilungsgraphen ${\displaystyle TG}$ eines Graphen ${\displaystyle G}$, so nennt man ${\displaystyle G}$ einen topologischen Minor von ${\displaystyle Z}$.

Folgende Definitionen finden sich auch gelegentlich in der Literatur:

Minor

Ein Graph ${\displaystyle G}$ heißt Minor von ${\displaystyle Z}$, wenn ${\displaystyle Z}$ einen Teilgraph enthält, aus dem durch Kantenkontraktion ${\displaystyle G}$ hervorgeht.

Topologischer Minor

Ein Graph ${\displaystyle G}$ heißt topologischer Minor von ${\displaystyle Z}$, wenn ${\displaystyle Z}$ einen Unterteilungsgraphen von ${\displaystyle G}$ enthält.

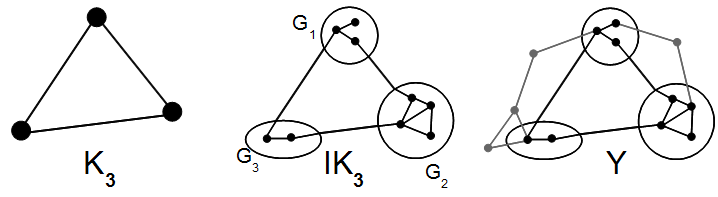
Links außen ist der vollständige Graph mit drei Knoten ${\displaystyle K_{3}}$ abgebildet. Dieser entsteht durch Kantenkontraktion aus dem Graphen ${\displaystyle IK_{3}}$, der wiederum in ${\displaystyle Y}$ enthalten ist. ${\displaystyle K_{3}}$ ist also ein Minor von ${\displaystyle Y}$.

Links außen ist der vollständige Graph mit drei Knoten, mittig ein Unterteilungsgraph abgebildet. Der Unterteilungsgraph ist aber im Graphen ${\displaystyle Z}$ enthalten, ${\displaystyle K_{3}}$ ist also topologischer Minor von ${\displaystyle Z}$.

• Die Minorenrelation ${\displaystyle G\preccurlyeq H:\Longleftrightarrow G{\text{ ist Minor von }}H}$ definiert eine Ordnungsrelation auf den endlichen Graphen, das heißt, sie ist reflexiv, transitiv und antisymmetrisch.
• Jeder Teilgraph eines Graphen ist auch ein Minor dieses Graphen.
• Jedes ${\displaystyle TX}$ ist auch ein ${\displaystyle IX}$. Damit ist jeder topologische Minor auch ein gewöhnlicher Minor.
• Nicht jeder Minor ist auch ein topologischer Minor. Ein Beispiel dafür ist der Petersen-Graph mit seinem Minor ${\displaystyle K_{5}}$.
• Die Minorenrelation definiert eine Wohlquasiordnung auf den endlichen Graphen. Dieser Satz ist auch als Minorentheorem bekannt.
• Die Determinante der Adjazenzmatrix eines Minors ist gerade der dem Teilgraphen entsprechende Minor im Sinne der Matrizenrechnung der Adjazenzmatrix des ursprünglichen Graphen.

Ein Graph ${\displaystyle H}$ wird als topologischer Minor eines Graphen ${\displaystyle G}$ bezeichnet, wenn ein Unterteilungsgraph von ${\displaystyle H}$ isomorph zu einem Teilgraphen von ${\displaystyle G}$ ist. Es ist leicht zu erkennen, dass jeder topologische Minor auch ein Minor ist. Die Umkehrung trifft jedoch im Allgemeinen nicht zu, gilt aber für Graphen mit einem maximalen Knotengrad von höchstens 3. Der vollständige Graph ${\displaystyle K_{5}}$ im Petersen-Graph ist ein Minor, aber kein topologischer Minor. Die topologische Minorenrelation ist keine Wohlquasiordnung auf der Menge der endlichen Graphen, und daher gilt das Minorentheorem von Robertson und Seymour nicht für topologische Minoren.^[1]

Ein Graph ${\displaystyle H}$ wird als induzierter Minor eines Graphen ${\displaystyle G}$ bezeichnet, wenn er aus einem induzierten Teilgraphen von ${\displaystyle G}$ durch Zusammenziehen von Kanten erhalten werden kann. Ansonsten wird er ${\displaystyle H}$-induziert und minorenfrei genannt.

Eine Graphenoperation, die als Heben bezeichnet wird, ist zentral in einem Konzept, das als Immersion bezeichnet wird. Das Heben erfolgt an benachbarten Kanten. Bei drei Knoten ${\displaystyle v,u}$ und ${\displaystyle w}$, wobei ${\displaystyle (v,u)}$ und ${\displaystyle (u,w)}$ Kanten im Graphen sind, ist das Heben von ${\displaystyle vuw}$ oder das Äquivalent von ${\displaystyle (v,u),(u,w)}$ die Operation, die die beiden Kanten ${\displaystyle (v,u)}$ und ${\displaystyle (u,w)}$ entfernt und die Kante ${\displaystyle (v,w)}$ hinzufügt. In dem Fall, in dem ${\displaystyle (v,w)}$ bereits vorhanden war, werden die Knoten ${\displaystyle v}$ und ${\displaystyle w}$ nun durch mehr als eine Kante verbunden, und daher ist diese Operation an sich eine Multigraphenoperation.

In dem Fall, in dem ein Graph ${\displaystyle H}$ aus einem Graphen ${\displaystyle G}$ durch eine Folge von Hebeoperationen erhalten werden kann und dann ein isomorpher Teilgraph gefunden wird, sagen wir, dass ${\displaystyle H}$ ein Immersionsminor von ${\displaystyle G}$ ist. Es gibt noch eine andere Möglichkeit, die Immersionsminoren zu definieren, die äquivalent zur Hebeoperation ist. Wir sagen, dass ${\displaystyle H}$ ein Immersionsminor von ${\displaystyle G}$ ist, wenn es eine injektive Abbildung von Knoten in ${\displaystyle H}$ zu Knoten in ${\displaystyle G}$ gibt, bei denen die Bilder benachbarter Elemente von ${\displaystyle H}$ in ${\displaystyle G}$ durch kantendisjunkte Pfade verbunden sind.

Die Immersionsminoren-Relation ist eine Wohlquasiordnung auf der Menge der endlichen Graphen, und daher gilt das Minorentheorem von Robertson und Seymour für Immersionsminoren.

Beim Graphzeichnen entstehen Immersionsminoren als Planarisierungen nichtplanarer Graphen: Aus einer Zeichnung eines Graphen in der Ebene mit Kreuzungspunkten kann ein Immersionsminor gebildet werden, indem jeder Kreuzungspunkt durch einen neuen Knoten ersetzt wird, und dabei auch jede gekreuzte Kante in einen Pfad unterteilt wird. Dadurch können Zeichenmethoden für planare Graphen auf nicht planare Graphen erweitert werden.^[2]

Eine alternative und äquivalente Definition von Minoren ist, dass ${\displaystyle H}$ ein Minor von ${\displaystyle G}$ ist, wenn die Knoten von ${\displaystyle H}$ durch eine Sammlung von knotendisjunkten Teilbäumen von ${\displaystyle G}$ dargestellt werden können, so dass, wenn zwei Knoten in ${\displaystyle H}$ benachbart sind, eine Kante mit seinen Endknoten in den entsprechenden zwei Bäumen in ${\displaystyle G}$ existiert.

Ein ungerader Minor schränkt diese Definition ein, indem diesen Teilbäumen Paritätsbedingungen hinzugefügt werden. Wenn ${\displaystyle H}$ wie oben durch eine Sammlung von Teilbäumen von ${\displaystyle G}$ dargestellt wird, ist ${\displaystyle H}$ ein ungerader Minor von ${\displaystyle G}$, wenn es möglich ist, den Knoten von ${\displaystyle G}$ zwei Farben so zuzuweisen, dass jede Kante von ${\displaystyle G}$ innerhalb eines Teilbaums richtig gefärbt ist, denn ihre Endknoten haben unterschiedliche Farben, und jede Kante von ${\displaystyle G}$, die eine Nachbarschaft zwischen zwei Teilbäumen darstellt, ist monochromatisch, d. h., beide Endknoten haben dieselbe Farbe. Anders als bei der üblichen Art von Minoren sind Graphen mit verbotenen ungeraden Minoren nicht unbedingt dünn.^[3] Die Vermutung von Hadwiger, dass ${\displaystyle k}$-chromatische Graphen notwendigerweise vollständige Graphen mit ${\displaystyle n}$ Knoten als Minoren enthalten, wurde auch unter dem Gesichtspunkt ungerader Minoren untersucht.^[4]

Eine andere Erweiterung der Definition von Minoren ist das Konzept eines bipartiten Minoren, der einen bipartiten Graphen erzeugt, wenn der ursprüngliche Graph bipartit ist. Ein Graph ${\displaystyle H}$ ist ein bipartiter Minor eines anderen Graphen ${\displaystyle G}$, wenn ${\displaystyle H}$ aus ${\displaystyle G}$ erhalten werden kann, indem Knoten entfernt, Kanten entfernt und Kantenkontraktionen durchgeführt werden, die entlang eines peripheren Zyklus des Graphen den Abstand 2 voneinander haben. Eine Form des Satzes von Wagner gilt für bipartite Minoren: Ein bipartiter Graph ist genau dann ein planarer Graph, wenn er den vollständig bipartiten Graphen ${\displaystyle K_{3,3}}$ nicht als bipartiten Minoren hat.^[5]

• Lutz Volkmann: Fundamente der Graphentheorie. Springer (Wien) 1996, ISBN 3-211-82774-9.
  Neuere Online-Version: Graphen an allen Ecken und Kanten. (PDF; 3,5 MB).
• Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (Online-Version). 

• Eric W. Weisstein: Graph Minor. In: MathWorld (englisch).
• N. N.: Minor of a graph. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org). Vorlage:EoM/id
• Minor eines Graphen. In: Lexikon der Mathematik.

1. ↑ Guoli Ding: Excluding a long double path minor. In: Journal of Combinatorial Theory. Band 66, Nr. 1, 1996, S. 11–23, doi:10.1006/jctb.1996.0002. 
2. ↑ Christoph Buchheim, Markus Chimani, Carsten Gutwenger, Michael Jünger, Petra Mutzel: Handbook of Graph Drawing and Visualization. CRC Press, Boca Raton, FL 2014. 
3. ↑ Ken-ichi Kawarabayashi, Yusuke Kobayashi, Bruce Reed: The disjoint paths problem in quadratic time. In: Journal of Combinatorial Theory. Band 102, Nr. 2, März 2012, S. 424–435, doi:10.1016/j.jctb.2011.07.004. 
4. ↑ Jim Geelen, Bert Gerards, Bruce Reed, Paul Seymour, Adrian Vetta: On the odd-minor variant of Hadwiger's conjecture. In: Journal of Combinatorial Theory. Band 99, Nr. 1, 2009, S. 20–29, doi:10.1016/j.jctb.2008.03.006. 
5. ↑ Maria Chudnovsky, Gil Kalai, Eran Nevo, Isabella Novik, Paul Seymour: Bipartite minors. In: Journal of Combinatorial Theory. Band 116, 2016, S. 219–228, doi:10.1016/j.jctb.2015.08.001, arxiv:1312.0210.