Klein paradox

In relativistic quantum mechanics, the Klein paradox (also known as Klein tunneling) is a quantum phenomenon related to particles encountering high-energy potential barriers. It is named after physicist Oskar Klein who discovered in 1929.^[1] Originally, Klein obtained a paradoxical result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping. However, Klein's result showed that if the potential is at least of the order of the electron mass ${\displaystyle Ve\approx mc^{2}}$ (where V is the electric potential, e is the elementary charge, m is the electron mass and c is the speed of light), the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.

The immediate application of the paradox was to Rutherford's proton–electron model for neutral particles within the nucleus, before the discovery of the neutron. The paradox presented a quantum mechanical objection to the notion of an electron confined within a nucleus.^[2] This clear and precise paradox suggested that an electron could not be confined within a nucleus by any potential well. The meaning of this paradox was intensely debated by Neils Bohr and others at the time.^[2]

The Klein paradox is an unexpected consequence of relativity on the interaction of quantum particles with electrostatic potentials. The quantum mechanical problem of free particles striking an electrostatic step potential has two solutions when relativity is ignored. One solution applies when the particles approaching the barrier have less kinetic energy than the step: the particles are reflected. If the particles have more energy than the step, some are transmitted past the step, while some are reflected. The ratio of reflection to transmission depends on the energy difference. Relativity adds a third solution: very steep potential steps appear to create particles and antiparticles that then change the calculated ratio of transmission and reflection. The theoretical tools called quantum mechanics cannot handle the creation of particles, making any analysis of the relativistic case suspect.^[3] Before antiparticles where discovered and quantum field theory developed, this third solution was not understood. The puzzle came to be called the Klein paradox.^[4]

The electric field strength required to observe the effect is enormous. The electric potential energy change similar to the rest energy of the incoming particle, ${\displaystyle mc^{2}}$, would need to occur over the Compton wavelength of the particle, ${\displaystyle \hbar m/c}$, which works out to 10¹⁶ V/cm for electrons.^[5] For electrons, such extreme fields might only be relevant in Z>170 nuclei or evaporation at the event horizon of black holes, but for 2-D quasiparticles at graphene p-n junctions the effect can be studied experimentally.^{[5][6]: 421}

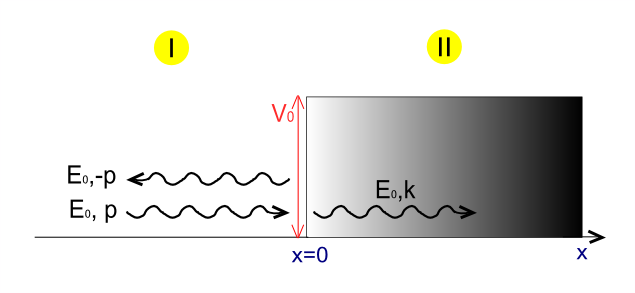
Consider a massless relativistic particle approaching a potential step of height ${\displaystyle V_{0}}$ with energy ${\displaystyle E_{0}<V_{0}e}$ and momentum ${\displaystyle p}$.

The particle's wave function, ${\displaystyle \psi }$, follows the time-independent Dirac equation:

${\displaystyle \left(\sigma _{x}p+V\right)\psi =E_{0}\psi ,\quad V={\begin{cases}0,&x<0\\V_{0},&x>0\end{cases}}}$

And ${\displaystyle \sigma _{x}}$ is the Pauli matrix:

${\displaystyle \sigma _{x}=\left({\begin{matrix}0&1\\1&0\end{matrix}}\right)}$

Assuming the particle is propagating from the left, we obtain two solutions — one before the step, in region (1) and one under the potential, in region (2):

${\displaystyle \psi _{1}=Ae^{ipx}\left({\begin{matrix}1\\1\end{matrix}}\right)+A'e^{-ipx}\left({\begin{matrix}-1\\1\end{matrix}}\right),\quad p=E_{0}\,}$

${\displaystyle \psi _{2}=Be^{ikx}\left({\begin{matrix}1\\1\end{matrix}}\right),\quad \left|k\right|=V_{0}-E_{0}\,}$

where the coefficients A, A′ and B are complex numbers. Both the incoming and transmitted wave functions are associated with positive group velocity (Blue lines in Fig.1), whereas the reflected wave function is associated with negative group velocity. (Green lines in Fig.1)

We now want to calculate the transmission and reflection coefficients, ${\displaystyle T,R.}$ They are derived from the probability amplitude currents.

The definition of the probability current associated with the Dirac equation is:

${\displaystyle J_{i}=\psi _{i}^{\dagger }\sigma _{x}\psi _{i},\ i=1,2\,}$

In this case:

${\displaystyle J_{1}=2\left[\left|A\right|^{2}-\left|A'\right|^{2}\right],\quad J_{2}=2\left|B\right|^{2}\,}$

The transmission and reflection coefficients are:

${\displaystyle R={\frac {\left|A'\right|^{2}}{\left|A\right|^{2}}},\quad T={\frac {\left|B\right|^{2}}{\left|A\right|^{2}}}\,}$

Continuity of the wave function at ${\displaystyle x=0}$, yields:

${\displaystyle \left|A\right|^{2}=\left|B\right|^{2}\,}$

${\displaystyle \left|A'\right|^{2}=0\,}$

And so the transmission coefficient is 1 and there is no reflection.

One interpretation of the paradox is that a potential step cannot reverse the direction of the group velocity of a massless relativistic particle. This explanation best suits the single particle solution cited above. Other, more complex interpretations are suggested in literature, in the context of quantum field theory where the unrestrained tunnelling is shown to occur due to the existence of particle–antiparticle pairs at the potential.

For the massive case, the calculations are similar to the above. The results are as surprising as in the massless case. The transmission coefficient is always larger than zero, and approaches 1 as the potential step goes to infinity.

If the energy of the particle is in the range ${\displaystyle mc^{2}<E<Ve-mc^{2}}$, then partial reflection rather than total reflection will result.

The traditional resolution uses particle–anti-particle pair production in the context of quantum field theory.^[7]

These results were expanded to higher dimensions, and to other types of potentials, such as a linear step, a square barrier, a smooth potential, etc. Many experiments in electron transport in graphene rely on the Klein paradox for massless particles.^[5][8]

• List of paradoxes

• Cheng, T.; Su, Q.; Grobe, R. (July 2010). "Introductory review on quantum field theory with space–time resolution". Contemporary Physics. 51 (4): 315–330. doi:10.1080/00107510903450559. ISSN 0010-7514.
• Dombey, N; Calogeracos, A. (July 1999). "Seventy years of the Klein paradox". Physics Reports. 315 (1–3): 41–58. Bibcode:1999PhR...315...41D. doi:10.1016/S0370-1573(99)00023-X.
• Robinson, T. R. (2012). "On Klein tunneling in graphene". American Journal of Physics. 80 (2): 141–147. Bibcode:2012AmJPh..80..141R. doi:10.1119/1.3658629.