McCay cubic

In Euclidean geometry, the McCay cubic (also called M'Cay cubic^[1] or Griffiths cubic^[2]) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003.^[2]

The McCay cubic can be defined by locus properties in several ways.^[2] For example, the McCay cubic is the locus of a point P such that the pedal circle of P is tangent to the nine-point circle of the reference triangle △ABC.^[3] The McCay cubic can also be defined as the locus of point P such that the circumcevian triangle of P and △ABC are orthologic.

The equation of the McCay cubic in barycentric coordinates ${\displaystyle x:y:z}$ is

${\displaystyle \sum _{\text{cyclic}}(a^{2}(b^{2}+c^{2}-a^{2})x(c^{2}y^{2}-b^{2}z^{2}))=0.}$

The equation in trilinear coordinates ${\displaystyle \alpha :\beta :\gamma }$ is

${\displaystyle \alpha (\beta ^{2}-\gamma ^{2})\cos A+\beta (\gamma ^{2}-\alpha ^{2})\cos B+\gamma (\alpha ^{2}-\beta ^{2})\cos C=0}$

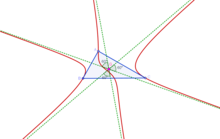
A stelloid is a cubic that has three real concurring asymptotes making 60° angles with one another. McCay cubic is a stelloid in which the three asymptotes concur at the centroid of triangle ABC.^[2] A circum-stelloid having the same asymptotic directions as those of McCay cubic and concurring at a certain (finite) is called McCay stelloid. The point where the asymptoptes concur is called the "radial center" of the stelloid.^[4] Given a finite point X there is one and only one McCay stelloid with X as the radial center.