Modélisation en Pi des lignes électriques

La modélisation en Pi des lignes électriques permet de représenter le comportement électrique attendu de celles-ci. Elle est basée sur les équations des télégraphistes. Le calcul des paramètres électriques utilisé pour la modélisation repose sur les équations de Maxwell. Le modèle avec une seule section en Pi n'est valable que pour de faibles fréquences et des lignes électriques courtes, dans le cas contraire plusieurs sections en Pi doivent être connectées en série.

Une portion de ligne électrique peut être représentée par le quadripole ci-contre où

• La résistance linéique (par unité de longueur) ${\displaystyle R}$ du conducteur est représentée par une résistance série (exprimée en ohms par unité de longueur).
• L'inductance linéique ${\displaystyle L}$ est représentée par une self (Henry par unité de longueur).
• La capacité linéique ${\displaystyle C}$ entre les 2 conducteurs est représentée par un condensateur C shunt (Farad par unité de longueur).
• La conductance linéique ${\displaystyle G}$ du milieu diélectrique séparant les 2 conducteurs est représentée par une résistance shunt (Siemens par unité de longueur). La résistance dans ce modèle a une valeur de ${\displaystyle 1/G}$ ohms.

Dans ce modèle, on définit la tension en tout point éloigné d'une distance x du début de la ligne et à tout instant t la tension ${\displaystyle U(x,t)}$ et le courant ${\displaystyle I(x,t)}$. Les équations s'écrivent :

${\displaystyle {\frac {\partial U}{\partial x}}(x,t)=-L{\frac {\partial I}{\partial t}}(x,t)-RI(x,t)}$

${\displaystyle {\frac {\partial I}{\partial x}}(x,t)=-C{\frac {\partial U}{\partial t}}(x,t)-GU(x,t)}$

De la formulation ci-dessus, on peut tirer 2 équations aux dérivées partielles ne faisant chacune intervenir qu'une variable :

${\displaystyle {\frac {\partial ^{2}U}{\partial x^{2}}}(x,t)=LC{\frac {\partial ^{2}U}{\partial t^{2}}}(x,t)+(RC+GL){\frac {\partial U}{\partial t}}(x,t)+GRU(x,t)}$

${\displaystyle {\frac {\partial ^{2}I}{\partial x^{2}}}(x,t)=LC{\frac {\partial ^{2}I}{\partial t^{2}}}(x,t)+(RC+GL){\frac {\partial I}{\partial t}}(x,t)+GRI(x,t)}$

En considérant les pertes, l'impédance Zl et l'admittance Yq se calculent comme suit ^[1]:

${\displaystyle Z_{l}=\Gamma \cdot \sinh(\gamma \cdot l)}$

${\displaystyle {\frac {Y_{q}}{2}}={\frac {1}{\Gamma }}\tanh \left(\gamma \cdot {\frac {l}{2}}\right)}$

Avec ${\displaystyle \gamma =\alpha +j\mathrm {B} ={\sqrt {Z'\cdot Y'}}}$ la constante de propagation, avec Z' l'impédance linéique de la ligne et Y' l'admittance linéique de la ligne. Et ${\displaystyle \Gamma ={\sqrt {\frac {Z'}{Y'}}}}$, l'impédance de la ligne. l est la longueur de la ligne.

Pour une ligne sans perte :

${\displaystyle Z_{l}=\Gamma \cdot j\cdot \sin(\mathrm {B} \cdot l)}$

${\displaystyle {\frac {Y_{q}}{2}}={\frac {1}{\Gamma }}j\cdot \tan \left(\mathrm {B} \cdot {\frac {l}{2}}\right)}$

Pour une ligne aérienne courte, inférieure à 80 km, on peut négliger les capacitances et simplifier l'impédance ^[2]:

${\displaystyle Z_{l}=Z'\cdot l}$

${\displaystyle {\frac {Y_{q}}{2}}=0}$ ou ${\displaystyle {\frac {Y_{q}}{2}}={\frac {Y'\cdot l}{2}}}$

Une section en Pi n'est constituée que d'éléments concentrés. Avec une seule section, le modèle en Pi n'est valable qu'en basse fréquence pour de faible longueur de ligne. Quand la longueur ou la fréquence augmente, le nombre de sections en Pi à connecter en série pour avoir une modélisation correcte doit être augmenté.

Une ligne peut être considérée comme "courte", c'est-à-dire modélisable avec une seule section en Pi, jusqu'à 200 km pour une ligne aérienne en 50 Hz et de 100 km pour un cable. Le nombre de sections en Pi doit augmenter proportionnellement avec la fréquence et inversement proportionnel à la longueur de ligne^[3],[2].

Les lignes à haute tension, surtout à plus de 220 kV, ne possèdent pas un conducteur unique par phase, mais de faisceaux de conducteurs en contenant de 2 à 4 (voir image ci-contre). Il est possible de modéliser un faisceau de conducteurs par un conducteur équivalent de rayon ^[4]:

${\displaystyle r_{\text{equivalent}}={\sqrt[{n}]{n\cdot r_{C}\cdot r_{T}^{n-1}}}}$

Où r_equivalent est le rayon équivalent du faisceau, r_C le rayon des conducteurs, r_T le rayon du cercle formé par le faisceau, n le nombre de conducteurs par faisceau (voir image).

Pour un système triphasé, il est possible de définir une distance équivalente entre les conducteurs, ou faisceaux de conducteurs selon le cas, en calculant la moyenne géométrique^{[anglais 1]}. Dans le cas d'un système triphasé simple, elle vaut^[5] :

${\displaystyle D={\sqrt[{3}]{D_{12}\cdot D_{23}\cdot D_{31}}}}$

Pour le cas d'un système double (deux lignes triphasés de chaque côté du pylône)^[5] :

${\displaystyle D={\sqrt[{3}]{D_{12}\cdot D_{23}\cdot D_{31}\cdot {\frac {D_{12'}\cdot D_{23'}\cdot D_{31'}}{D_{11'}\cdot D_{22'}\cdot D_{33'}}}}}}$

La résistance linéaire d'un conducteur à 20 °C est^[6] :

${\displaystyle R_{20}={\frac {\rho }{S}}}$

Avec ${\displaystyle S}$ la section et ${\displaystyle \rho }$ la résistivité du matériau conducteur. Pour un conducteur en cuivre la résistivité est de l'ordre de 1,8 x 10^-8 Ω∙m pour de l'aluminium de 3 x 10^-8 Ω∙m^[6].

La résistance de la ligne dépend également de la température :

${\displaystyle R=R_{20}\cdot (1+\alpha \Delta T)}$

Où ${\displaystyle \alpha }$ est la coefficient de température et ${\displaystyle \Delta T}$ la différence en kelvins entre la température et 20 °C^[6].

Dans le cas d'un faisceaux de conducteurs, ces derniers étant en parallèle la résistance doit être divisée par le nombre de conducteurs.

L'inductance linéique d'une ligne vaut^[7] :

${\displaystyle L_{\text{ligne}}'={\frac {\mu _{0}}{2\pi }}\left(\ln \left({\frac {D}{r}}\right)+{\frac {\mu _{r}}{4n}}\right)}$

Avec n le nombre de conducteurs par faisceau et ${\displaystyle \mu _{r}}$ la permittivité du conducteur. Dans le cas ${\displaystyle \mu _{r}}$ est égal à 1, on peut définir un rayon équivalent ${\displaystyle r_{GMR}=r\cdot e^{-1/4n}}$^{[anglais 2]}:

${\displaystyle L_{\text{ligne}}'={\frac {\mu _{0}}{2\pi }}\ln \left({\frac {D}{r_{GMR}}}\right)}$

Démonstration

Deux conducteurs

Soit un système constitué d'une ligne aller et d'une ligne retour d'une longueur l, considérer comme très grande devant les autres distances, et espacées d'une distance d. En prenant un contour circulaire autour d'un conducteur de longueur ${\displaystyle 2\pi x}$ et en y appliquant le théorème d'Ampère on a^[8]:

${\displaystyle \oint Hdl=I_{\text{traversant}}}$

${\displaystyle H2\pi x=I_{\text{traversant}}}$

Pour ${\displaystyle x<r}$ (rayon du conducteur) on obtient : ${\displaystyle H={\frac {I\cdot x^{2}}{2\pi xr^{2}}}}$ Pour ${\displaystyle x\geqslant r}$ on obtient : ${\displaystyle H={\frac {I}{2\pi x}}}$

L'énergie contenue dans le conducteur W est égale à :

${\displaystyle W_{i}={\frac {1}{2}}\iiint {B\wedge H\cdot dV}}$

${\displaystyle W_{i}={\frac {1}{2}}\iiint \mu _{i}H^{2}dV}$

Où ${\displaystyle \mu _{i}}$ est la perméabilité magnétique du conducteur.

${\displaystyle W_{i}={\frac {1}{2}}\int _{0}^{r}\mu _{i}\left({\frac {I_{1}x}{2\pi r^{2}}}\right)^{2}l2\pi xdx}$

[...]

${\displaystyle W_{i}=I_{1}^{2}{\frac {\mu _{i}l}{16\pi }}}$

Or

${\displaystyle W_{i}={\frac {1}{2}}L_{i}I^{2}}$

avec L_i l'inductance interne du conducteur.

Donc

${\displaystyle L_{i}={\frac {\mu _{i}l}{8\pi }}}$

En linéique

${\displaystyle L_{i}'={\frac {\mu _{i}}{8\pi }}}$

Maintenant que l'inductance interne est connue, il reste à déterminer l'inductance externe. On prend en compte le champ créé par un seul conducteur entre lui et l'autre conducteur (où le champ s'annule):

${\displaystyle \Phi =\iint B\cdot dS=\iint \mu _{a}H\cdot dS=\int _{r}^{d}\mu _{a}{\frac {I}{2\pi x}}ldx}$

${\displaystyle \Phi =\mu _{a}{\frac {I}{2\pi }}l\ln \left({\frac {d}{r}}\right)}$

Or

${\displaystyle L_{a}={\frac {\Phi }{I}}=\mu _{a}{\frac {1}{2\pi }}l\ln \left({\frac {d}{r}}\right)}$

Avec ${\displaystyle \Phi }$ le flux magnétique. En linéique :

${\displaystyle L_{a}'=\mu _{a}{\frac {1}{2\pi }}\ln \left({\frac {d}{r}}\right)}$

L'inductance totale extérieure étant celle provoquée par le conducteur aller et le conducteur retour, et l'inductance interne se sommant également on a:

${\displaystyle L_{\text{totale}}'=2L_{a}'+2L_{i}}$

En considérant un perméabilité magnétique égale ${\displaystyle \mu _{r}}$, l'équation devient:

${\displaystyle L_{\text{totale}}'={\frac {\mu _{0}}{\pi }}\left({\frac {\mu _{r}}{4}}+\ln \left({\frac {d}{r}}\right)\right)}$

Système triphasé

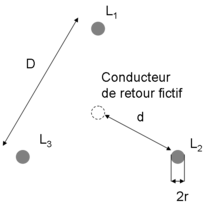
Pour un système triphasé on considère un conducteur de retour fictif situé entre les 3 phases. Les équations ci-dessus sont encore applicables, il faut de plus calculer les inductances mutuelles entre phases^[8]. Attention les conducteurs sont simples ici, pour le détails avec des faisceaux de conducteur se référer à la note^[7].

${\displaystyle M_{31}={\frac {\Phi _{1}}{I_{3}}}={\frac {1}{I_{3}}}\iint B_{1}dS}$

Avec B₁ le champ appliqué sur le conducteur 1 par le courant traversant le conducteur 3.

${\displaystyle M_{31}={\frac {\mu _{0}l}{2\pi I_{3}}}\left[I_{3}\left({\frac {\mu _{r}}{4}}+\int _{r}^{d}{\frac {1}{x}}dx\right)-I_{3}\int _{d}^{D}{\frac {1}{x}}dx\right]}$

À partir de d, le conducteur du retour influence le champ. On obtient donc :

${\displaystyle M_{31}={\frac {\mu _{0}l}{2\pi }}\left({\frac {\mu _{r}}{4}}+\ln \left({\frac {d}{r}}\right)+\ln \left({\frac {D}{d}}\right)\right)}$

${\displaystyle M_{31}={\frac {\mu _{0}l}{2\pi }}\left({\frac {\mu _{r}}{4}}+\ln \left({\frac {d^{2}}{r\cdot D}}\right)\right)}$

Le système étant symétrique M₁₂=M₂₃=M₃₁=M.

L'inductance d'une ligne, L_ligne est donc régie par l'équation suivante :

${\displaystyle L_{\text{ligne}}I_{1}=L_{\text{totale}}I_{1}+MI_{2}+MI_{3}}$

Le système étant triphasé ${\displaystyle I_{1}+I_{2}+I_{3}=0}$. D'où :

${\displaystyle L_{\text{ligne}}I_{1}=L_{\text{totale}}I_{1}-MI_{1}}$

En simplifiant (en linéique):

${\displaystyle L_{\text{ligne}}'=L_{\text{totale}}'-M={\frac {\mu _{0}}{2\pi }}\left[2\left({\frac {\mu _{r}}{4}}+\ln \left({\frac {d}{r}}\right)\right)-\left({\frac {\mu _{r}}{4}}+\ln \left({\frac {d^{2}}{r\cdot D}}\right)\right)\right]}$

${\displaystyle L_{\text{ligne}}'={\frac {\mu _{0}}{2\pi }}\left(\ln \left({\frac {D}{r}}\right)+{\frac {\mu _{r}}{4}}\right)}$

Le professeur Thierry Van Cutsem propose une démonstration légèrement différente, voir la note^[7].

 

Ci-dessous quelques valeurs typique pour un réseau 50 Hz avec des conducteurs aluminium / acier de section d'aluminium 240 mm² et d'acier 40 mm^2[9],[10].

D'autres valeurs pour la résistance seulement^[7] :

Et l'inductance^[7] :

Dans un système triphasé, il y a des capacités entre les lignes et la terre, mais également entre lignes. L'objectif est de synthétiser le tout dans une seule capacité "moyenne" C_b égale pour les trois lignes :

${\displaystyle C_{b}'={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln \left({\dfrac {D}{r}}\right)}}}$

Dans laquelle les ${\displaystyle \epsilon _{0}}$ et ${\displaystyle \epsilon _{r}}$ sont les permittivité diélectrique du vide et du matériau (dans le cas de l'air pour les lignes ${\displaystyle \epsilon _{r}}$ vaut environ 1).

On peut démontrer en utilisant le théorème de Kennelly que^[7] :

${\displaystyle C_{b}'=3\cdot C_{L}+C_{T}}$

Avec C_L la capacité mutuelle et C_T la capacité à la terre

Démonstration

Afin de modéliser le potentiel nul de la terre, on utilise le principe des miroirs. C'est-à-dire qu'on modélise des conducteurs fictifs placés de manière symétrique à la terre par rapport aux conducteurs réels et chargés de manière opposée. La terre a alors un potentiel nul.

Soit le cas représenté ci-contre d'un seul conducteur. Le potentiel d'un point Pi arbitraire, distant de a_ij du conducteur réel et de a_ij* du conducteur fictif est d'après le théorème de Gauss^[11] :

${\displaystyle V_{P}=V_{P,{\text{causé par conducteur réel}}}+V_{P,{\text{causé par conducteur fictif}}}}$

${\displaystyle V_{P}={\frac {Q_{j}'}{2\pi \epsilon _{0}\epsilon _{r}}}\ln \left({\frac {1}{a_{ij}}}\right)-{\frac {Q_{j}'}{2\pi \epsilon _{0}\epsilon _{r}}}\ln \left({\frac {1}{a_{ij*}}}\right)}$

${\displaystyle V_{P}={\frac {Q_{j}'}{2\pi \epsilon _{0}\epsilon _{r}}}\ln \left({\frac {a_{ij}*}{a_{ij}}}\right)}$

Le même principe est utilisé pour un système triphasé. Pour chaque point P on a alors l'équation:

${\displaystyle V_{P}={\frac {1}{2\pi \epsilon _{0}\epsilon _{r}}}\left(Q_{1}'\ln \left({\frac {a_{1j}*}{a_{1j}}}\right)+Q_{1}'\ln \left({\frac {a_{2j}*}{a_{2j}}}\right)+Q_{1}'\ln \left({\frac {a_{3j}*}{a_{3j}}}\right)\right)}$

En plaçant les pointsi P sur les conducteurs 1, 2 et 3, les potentiels valent alors U₁, U₂ et U₃.

On peut présenter le problème précédent sous forme matricielle : U = M * Q. Avec U le vecteur des tensions des 3 conducteurs, Q les 3 charges et M une matrice constitué des ${\displaystyle {\frac {1}{2\pi \epsilon _{0}}}\ln \left({\frac {a_{1j}*}{a_{1j}}}\right)}$ pour i et j allant de 1 à 3.

Le système est considéré symétrique (voir commutation des phases) :

${\displaystyle C_{12}=C_{23}=C_{13}}$

Et

${\displaystyle C_{1T}=C_{2T}=C_{3T}}$

Une distance équivalente égale à la moyenne géométrique entre faisceaux est calculée avec la méthode présentée ci-dessus pour le système réel, notée D, et le système fictif, notée D*. Une hauteur moyenne géométrique est également définie :

${\displaystyle h={\sqrt[{3}]{h_{1}h_{2}h_{3}}}}$

Par ailleurs tous les conducteurs ont le même rayon r. Les termes ${\displaystyle {\frac {1}{2\pi \epsilon _{0}}}\ln \left({\frac {a_{1j}*}{a_{1j}}}\right)}$ diagonaux valent donc ${\displaystyle {\frac {1}{2\pi \epsilon _{0}}}\ln \left({\frac {2h}{r}}\right)=p_{A}}$ Et tous les autres termes ${\displaystyle {\frac {1}{2\pi \epsilon _{0}}}\ln \left({\frac {D*}{D}}\right)=p_{B}}$.

En résolvant le système matriciel, on obtient : ${\displaystyle Q_{i}={\frac {1}{p_{A}-p_{B}}}\cdot U_{i}}$ avec i=1..3.

${\displaystyle {\frac {1}{p_{A}-p_{B}}}={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln({\frac {2h}{r}})-\ln({\frac {D*}{D}})}}}$

${\displaystyle {\frac {1}{p_{A}-p_{B}}}={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln({\frac {2hD}{rD*}})}}}$

En approximant D* par ${\displaystyle {\sqrt {(2h)^{2}+D^{2}}}}$, on obtient :

${\displaystyle {\frac {1}{p_{A}-p_{B}}}={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln \left({\frac {D}{r{\sqrt {1+({\frac {D}{2h}})^{2}}}}}\right)}}}$

${\displaystyle D<<2h}$ d'où :

${\displaystyle {\frac {1}{p_{A}-p_{B}}}={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln({\frac {D}{r}})}}}$

Par définition :

${\displaystyle C_{b}'={\frac {Q_{1}'}{U_{1}}}={\frac {1}{p_{A}-p_{B}}}={\frac {2\pi \epsilon _{0}\epsilon _{r}}{\ln({\frac {D}{r}})}}}$

 

Une résistance doit être représentée en parallèle aux capacités pour être complet. Elle est due au effet corona et aux fuites de courant (causées par la pollution sur les isolateurs par exemple). Pour une ligne de 380 kV elle vaut^[12] :

Ci-dessous quelques valeurs typiques pour un réseau 50 Hz^[13].

Pour les câbles, les calculs de résistance et d'inductivité sont identiques^[14]. La capacité vaut :

${\displaystyle C_{T}=C_{b}'={\frac {2\pi \epsilon }{\ln({\frac {r_{2}}{r_{1}}})}}}$

Avec r₁ le rayon de l'âme et r₂ le rayon intérieur de l'écran. La capacité entre les lignes est négligeable.

La conductance est égale à^[14]:

${\displaystyle G_{b}'=\tan(\delta )\cdot \omega C_{b}'}$

Quelques valeurs typiques^{[14],[7],[15]} :

Type d'isolation du câble	${\displaystyle tan(\delta )}$	${\displaystyle \epsilon _{r}}$
Papier imprégné	2 - 3 10−3	3,3-3,5
PVC		3,5 - 8,0
Éthylène propylène		2,8 - 3,5
Polyéthylène	0,2 - 0,5 10−3	2,2-2,3
Polyéthylène réticulé		2,3 - 6

La norme IEC 60287-1-1 fournit de nombreuses formules pour le calcul des paramètres électriques des câbles.

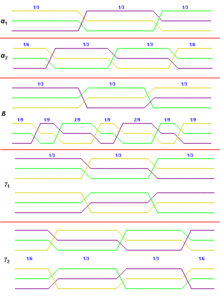
La capacité ligne-terre dépend de la hauteur à laquelle se trouve le conducteur ou faisceau de conducteur. Dans les exemples précédents, un de ces conducteurs se trouve plus haut que les deux autres. Si rien n'est fait, la capacité de cette phase vis-à-vis de la terre serait différente de celle des deux autres phases, ce qui n'est pas souhaitable pour un système triphasé symétrique^[12],[7].

Pour résoudre le problème, on commute les phases entre elles à intervalle régulier au moyen d'un pylône de transposition. Pour des lignes d'une longueur inférieure à 200 km deux transpositions, ce qui permet à chaque ligne d'avoir en moyenne le même comportement capacitif, suffisent^[12]. Les courants induits par les trois phases se compensent alors.

• angle de transport

• (de) Joseph Kindersberger, Grundlagen der Hochspannungs- und Energieübertragungstechnik, TU Munich, 2009

• IEC 60287-1-1 Câbles électriques – Calcul du courant admissible – Partie 1-1: Equations de l’intensité du courant admissible (facteur de charge 100 %) et calcul des pertes – Généralités, 2006
• CIGRÉ Brochure 531 Cable Systems Electrical Characteristics, 2013

• « Présentation de l'université Laval sur les lignes à haute tension » (consulté le 12 janvier 2013)

• Portail de l’électricité et de l’électronique
• Portail de l’énergie