Orthoptique

Ne doit pas être confondu avec Orthoptie.
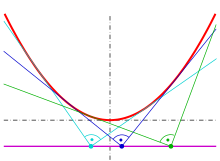

En géométrie, une orthoptique est l'ensemble des points pour lesquels deux tangentes d'une courbe donnée se rencontrent à angle droit.
Plus généralement, une isoptique est l'ensemble des points pour lesquels deux tangentes d'une courbe donnée se rencontrent selon un angle fixe.
Le théorème de Thalès sur une corde PQ peut être considéré comme l'orthoptique de deux cercles dégénérés aux deux points P et Q .
Exemples d'orthoptiques
Orthoptique d'une parabole
Toute parabole peut être transformée par un mouvement rigide (les angles ne sont pas modifiés) en une parabole d'équation . La pente en un point de cette parabole est . Remplacer donne la représentation paramétrique de la parabole avec la pente tangente comme paramètre : La tangente a pour équation avec le paramètre encore inconnu , qui peut être déterminé en insérant les coordonnées du point de la parabole. On obtient
Si une tangente contient le point (x0, y0), hors de la parabole, alors l'équation
est vraie, qui admet deux solutions m1 et m2 correspondant aux deux tangentes passant par (x0, y0). Le terme constant d'une équation quadratique réduite est toujours le produit de ses solutions. Par conséquent, si les tangentes se rencontrent en (x0, y0) orthogonalement, les équations suivantes s'appliquent :
La dernière équation est équivalente à
qui est l'équation de la directrice.
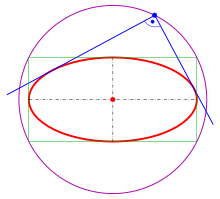
Orthoptique d'une ellipse et d'une hyperbole
Ellipse
Soit l'ellipse étudiée.
Les tangentes à l'ellipse aux sommets et les co-sommets se croisent aux 4 points , qui se situent sur la courbe orthoptique désirée (le cercle ).
La tangente en un point de l'ellipse a l'équation (voir tangente à une ellipse). Si le point n'est pas un sommet, cette équation peut être résolue pour y :
En notant et l'équation on obtient :
Ainsi et l'équation d'une tangente non verticale est
La résolution de relations pour et en respectant conduit à la représentation paramétrique dépendant de la pente de l'ellipse :
Si une tangente contient le point , hors de l'ellipse, alors on a l'équation

L'élimination de la racine carrée conduit à
qui a deux solutions correspondant aux deux tangentes passant par . Le terme constant d'une équation quadratique monique est toujours le produit de ses solutions. Donc, si les tangentes se rencontrent en orthogonalement, les équations suivantes sont vérifiées :
La dernière équation est équivalente à
Ainsi, les points d'intersection des tangentes orthogonales sont les points du cercle , qu'on appelle cercle de Monge de l'ellipse.
Hyperbole
Le cas de l'ellipse peut être adapté presque exactement au cas de l'hyperbole. Les seules modifications à apporter sont de remplacer par et restreindre m à |m| > b/a
Dans ce cas, les points d'intersection des tangentes orthogonales sont les points du cercle , où a > b.
Orthoptique d'un astroïde

Un astroïde peut être décrit par la représentation paramétrique
- .
De la condition
on reconnaît la distance α dans l'espace des paramètres à laquelle apparaît une tangente orthogonale à . Il s'avère que la distance est indépendante du paramètre t, à savoir α = ± π/2
Leur point commun a pour coordonnées :
Il s'agit en même temps d'une représentation paramétrique de l'orthoptique.
L'élimination du paramètre t donne la représentation implicite
En introduisant le nouveau paramètre φ = t − 5π/4, il vient
La preuve utilise les identités de somme et de différence d'angle. On obtient ainsi la représentation polaire de l'orthoptique :
Ainsi, l'orthoptique d'un astroïde est un quadrifolium.
Autres exemples
- L'orthoptique d'une cardioide est, selon les paramètres de la courbe, un cercle ou un limaçon.
- L'orthoptique d'une deltoïde est un cercle.
- L'orthoptique d'une spirale logarithmique est une spirale logarithmique de même paramètre.
Isoptiques
Isoptique de sections coniques


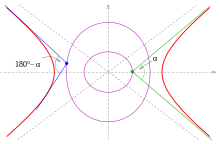
Ci-dessous, les isotopes pour les angles α ≠ 90° sont répertoriés. On les appelle α-isoptiques.
- Parabole
Les α -isoptiques de la parabole d'équation y = ax2 sont les branches de l'hyperbole
Les branches de l'hyperbole fournissent les isoptiques pour les deux angles α et 180° − α (voir image).
Une parabole y = ax2 peut être paramétrée par la pente de ses tangentes m = 2ax :
La tangente de pente m a pour équation
Le point (x0, y0) est sur la tangente si et seulement si
Cela signifie que les pentes m1, m2 des deux tangentes contenant (x0, y0) satisfont l'équation quadratique
Si les tangentes se rencontrent à un angle α ou 180° − α, l'équation
doit être remplie. En résolvant l'équation quadratique pour m, et en insérant m1, m2 dans la dernière équation, on obtient
C'est l'équation de l'hyperbole ci-dessus. Ses branches portent les deux isoptiques de la parabole pour les deux angles α et 180° − α.
- Ellipse
L'α-isoptique de l'ellipse d'équation
Dans le cas d'une ellipse
Maintenant, comme dans le cas d'une parabole, l'équation quadratique doit être résolue et les deux solutions m1, m2 doivent être insérées dans l'équation
Le réarrangement montre que les isoptiques font partie de la courbe de degré 4 :
- Hyperbole
L'α-isoptique de l'hyperbole d'équation
La solution pour le cas d'une hyperbole peut être adoptée à partir du cas de l'ellipse en remplaçant b2 par −b2 (comme dans le cas de l'orthoptique, voir ci- dessus ).
Pour visualiser les isoptiques, voir courbe implicite.
Autres exemples
- Une isoptique d'une épicycloïde est une épitrochoïde
- Une isoptique d'une hypocycloïde est une hypotrochoïde
- Une isoptique d'une spirale sinusoïdale est une autre spirale sinusoïdale
- Une isoptique d'une cycloïde est une autre cycloïde, allongée ou raccourcie
Références
- (en) Harold Hilton et R. E. Colomb, « On Orthoptic and Isoptic Loci », American Journal of Mathematics, vol. 39, no 1, , p. 86–94 (DOI 10.2307/2370445)
- (en) Waldemar Cieślak et Witold Mozgawa, « On curves with circles as their isoptics. », Aequat. Math., vol. 96, , p. 653–667 (DOI 10.1007/s00010-021-00828-4)
Liens externes
- Courbes planes spéciales.
- (en) Eric W. Weisstein, « Isoptic Curve », sur MathWorld
- Les courbes de Jan Wassenaar
- "Courbe isoptique" sur MathCurve
- "Courbe orthoptique" sur MathCurve
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Orthoptic (geometry) » (voir la liste des auteurs).
- J. Dennis Lawrence, A catalog of special plane curves, Dover Publications, , 58–59 (ISBN 0-486-60288-5, lire en ligne
 )
) - Odehnal, « Equioptic Curves of Conic Sections », Journal for Geometry and Graphics, vol. 14, no 1, , p. 29–43 (lire en ligne)
- Hermann Schaal, Lineare Algebra und Analytische Geometrie, vol. III, Vieweg, (ISBN 3-528-03058-5), p. 220
- Jacob Steiner, Vorlesungen über synthetische Geometrie, Leipzig, B. G. Teubner, (lire en ligne)
- Ternullo, « Two new sets of ellipse related concyclic points », Journal of Geometry, vol. 94, nos 1–2, , p. 159–173 (DOI 10.1007/s00022-009-0005-7, S2CID 120011519)
v · m Transformations différentielles des courbes planes | |
|---|---|
| Opération unaire | |
| Opération unaire définie par un point |
|
| Opération unaire définie par deux points | Strophoïde |
| Opération binaire définie par un point |
|
| Opérations sur une famille de courbes | Enveloppe |
 Portail de la géométrie
Portail de la géométrie



































































