Irányított körmentes gráf

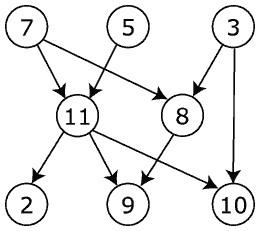
A számítógéptudományban és a matematikában az angol neve (directed acyclic graph) után DAG-nak is nevezett irányított körmentes gráf egyetlen irányított kört sem tartalmazó irányított gráf; ami azt jelenti, hogy egyetlen v csúcsához sincs abból induló és ugyanott végződő irányított út. DAG-ok alapvetően az olyan modellekben fordulnak elő, amelyben önmagába záródó úttal rendelkező csúcsnak nincs értelme, például ha egy u→v él azt jelenti, hogy v egy része u-nak, tehát ilyen út azt jelentené, hogy u önmaga része, ami értelmetlen.

Minden irányított körmentes gráfhoz megfeleltethető a csúcsai egy részbenrendezése, amelyben u ≤ v pontosan akkor áll fenn, ha a gráfban létezik u-ból v-be menő irányított út. Ugyanakkor egy ilyen részbenrendezést sok különböző irányított körmentes gráf is reprezentálhat. Ezek között a legkevesebb élt a tranzitív redukált, a legtöbbet a tranzitív lezárt tartalmazza.

A forrás a bejövő élt nem tartalmazó, a nyelő a kimenő élt nem tartalmazó csúcs. Egy véges DAG-nak legalább egy forrást, és legalább egy nyelőt tartalmaznia kell.

Egy véges DAG hossza a leghosszabb bejárható (irányított) út csúcsainak száma.

Minden irányított körmentes gráfnak van egy topológiai sorrendje, ami a csúcsainak egy olyan sorozata, amelyben minden csúcs a belőle elérhető csúcsok előtt szerepel. Ez a rendezés általában nem egyértelmű. Az azonos részleges rendezéssel reprezentált irányított körmentes gráfhoz tartozó topológiai rendezések halmaza is azonos.

A DAG-ok fák általánosításának is tekinthetők abból a szempontból, hogy a DAG-okban az egyes részfák a gráf különböző részein többször is előfordulhatnak. Egy sok azonos részfát tartalmazó fa esetén ez a struktúra méretének drasztikus csökkenését okozhatja. Ugyanakkor viszont a DAG-ok erdőkké bővíthetők a következő algoritmussal:

• Amíg létezik 1-nél nagyobb n bemeneti fokszámú v csúcs,
  • Hozzuk létre a v csúcs n darab másolatát úgy, hogy minden példány ugyanazokkal a kimeneti élekkel rendelkezzen, de bemenő élek nélkül,
  • Csatoljuk az eredeti v csúcs bemenő éleiből egyet-egyet az előbbi lépésben "másolt" csúcsokhoz,
  • Töröljük az eredeti v csúcsot.

Ha a gráfot változtatás, vagy a csúcsok egyenlőségének vizsgálata nélkül járjuk be, akkor a fenti módon létrejött erdő azonosnak fog tűnni a kiinduló DAG-gal.

Egyes algoritmusok sokkal egyszerűbbek általános gráfok helyett DAG-okra alkalmazva. Például a mélységi keresésen alapuló gráfalgoritmusok futtatásakor általában nyilván kell tartanunk a már bejárt csúcsokat. Erre azért van szükség, mert enélkül egy kör bejárásakor végtelen ciklusba juthatnánk. DAG-ok esetében nincsenek ilyen körök.

Az n csúcsú, nem-izomorf DAG-ok számát a Weisstein-sejtés^[1] adja meg: eszerint az n csúcsú, nem izomorf DAG-ok száma egyenlő a csak 0-t és 1-et tartalmazó n × n-es mátrixok számával, melyek sajátértékei pozitív valós számok. A sejtést McKay és társai bizonyították be.^[2]

Az irányított körmentes gráfokat sokféleképpen használja a számítástudomány:

• Bayes-hálók
• A szemétgyűjtő algoritmusok általában DAG-okkal tartják nyilván a referenciákat
• Parancs-ütemezés és makefile-ok függőségi gráfja
• Objektumorientált programozási nyelvekben az öröklődéssel létrehozott osztályok függőségi gráfjai
• Irányított körmentes szó-gráfok használhatóak sztring-halmazok (szó-halmazok) memóriatakarékos tárolására
• A Wikipédia kategóriarendszere is DAG-gal ábrázolható, amennyiben a kategóriaszervezési irányelvek tiltják az önmagukat tartalmazó kategórialáncok kialakítását, viszont engedélyezik, hogy egy kategória több fő-kategóriának is al-kategóriája lehessen.

• Weisstein, Eric W.: Acyclic Digraph (angol nyelven). Wolfram MathWorld