Grup selang-seling

Struktur aljabar → Teori grup Teori grup
Gagasan dasar Subgrup Subgrup normal Grup hasil bagi darab langsung semi-darab langsung Homomorfisme grup kernel bayangan jumlah langsung karangan bunga sederhana hingga takhingga kontinu multiplikatif aditif siklik Abel dihedral nilpoten terselesaikan aksi Glosarium teori grup Daftar topik teori grup
Grup hingga Klasifikasi grup sederhana hingga siklik bergantian tipe Lie sporadik Teorema Cauchy Teorema Lagrange Teorema Sylow Teorema Hall grup-p Grup Abel elementer Grup Frobenius Pengganda Schur Grup simetrik ${\displaystyle \mathrm {S} _{n}}$ Grup Klein ${\displaystyle \mathrm {V} }$ Grup dihedral ${\displaystyle \mathrm {D} _{n}}$ Grup kuaternion ${\displaystyle \mathrm {Q} }$ Grup disiklik ${\displaystyle \mathrm {Dic} _{n}}$
Grup diskret Kekisi Bilangan bulat (${\displaystyle \mathbb {Z} }$) Grup bebas Grup modular ${\displaystyle \mathrm {PSL} (2,\mathbb {Z} )}$ ${\displaystyle \mathrm {SL} (2,\mathbb {Z} )}$ Grup aritmetika Kekisi Grup hiperbolik
Topologis dan Grup Lie Solenoid Lingkaran Linear umum ${\displaystyle \mathrm {GL} (n)}$ Linear khusus ${\displaystyle \mathrm {SL} (n)}$ Ortogonal ${\displaystyle \mathrm {O} (n)}$ Euklides ${\displaystyle \mathrm {E} (n)}$ Ortogonal khusus ${\displaystyle \mathrm {SO} (n)}$ Uner ${\displaystyle \mathrm {U} (n)}$ Uniter khusus ${\displaystyle \mathrm {SU} (n)}$ Simplektik ${\displaystyle \mathrm {Sp} (n)}$ G2 F4 E6 E7 E8 Lorentz Poincaré konformal Difeomorfisme Gelung Grup Lie berdimensi takhingga ${\displaystyle O(\infty )}$ ${\displaystyle \mathrm {SU} (\infty )}$ ${\displaystyle \mathrm {Sp} (\infty )}$
Grup aljabar Grup aljabar linear Grup reduktif Varietas Abel Kurva eliptik
l b s

Dalam matematika, grup selang-seling (bahasa Inggris: Alternating group) adalah grup dari permutasi genap dari himpunan hingga. Grup selang-seling pada himpunan elemen ${\displaystyle n}$ disebut grup selang-seling derajat ${\displaystyle n}$, atau grup selang-seling pada huruf ${\displaystyle n}$ dan dilambangkan dengan ${\displaystyle \mathrm {A} _{n}}$ or ${\displaystyle \operatorname {Alt} (n)}$.

Sifat dasar

Untuk ${\displaystyle n>1}$, grup ${\displaystyle \operatorname {A} _{n}}$ adalah subgrup komutator dari grup simetris ${\displaystyle S_{n}}$ dengan indeks 2 dan karena itu memiliki ${\displaystyle {\frac {n!}{2}}}$ elemen (dimana ${\displaystyle !}$ melambangkan faktorial). Ini adalah kernel dari tanda tangan kehomomorfan grup ${\displaystyle \operatorname {sgn} \colon S_{n}\to \{1,-1\}}$ dijelaskan di bawah grup simetrik.

Grup ${\displaystyle \mathrm {A} _{n}}$ adalah abelian jika dan hanya jika ${\displaystyle n\leq 3}$ dan sederhana jika dan hanya jika ${\displaystyle n=3}$ atau ${\displaystyle n\geq 5}$. ${\displaystyle \mathrm {A} _{5}}$ adalah grup sederhana takAbel terkecil, memiliki urutan 60, dan grup takterpecahkan terkecil.

Grup ${\displaystyle \mathrm {A} _{4}}$ memiliki grup empat Klein ${\displaystyle V}$ sebagai subgrup normal wajar, yaitu identitas dan transposisi ganda ${\displaystyle \{(),(12)(34),(13)(24),(14,23)\}}$, itulah kernel dari surjeksi ${\displaystyle \mathrm {A} _{4}}$ ke ${\displaystyle \mathrm {A} _{3}=\mathrm {Z} _{3}}$. Kita memiliki urutan persis ${\displaystyle V\to \mathrm {A} _{4}\to \mathrm {A} _{3}=\mathrm {Z} _{3}}$. Dalam Teori Galois, peta ini, atau lebih tepatnya peta berpadanan ${\displaystyle \mathrm {S} _{4}\to \mathrm {S} _{3}}$, berpadanan dengan mengasosiasikan Penyelesai Lagrange kubik ke kuartik, yang memungkinkan polinomial kuartik untuk diselesaikan dengan radikal, seperti yang ditetapkan oleh Lodovico Ferrari.

Kelas konjugasi

Seperti dalam grup simetris, dua elemen ${\displaystyle \mathrm {A} _{n}}$ yang sekawan oleh elemen ${\displaystyle \mathrm {A} _{n}}$ harus memiliki bentuk siklus yang sama. Kebalikannya belum tentu benar. Jika bentuk siklus hanya terdiri dari siklus dengan panjang ganjil tanpa ada dua siklus yang panjangnya sama, dimana siklus dengan panjang satu dimasukkan ke dalam tipe siklus, maka tepat ada dua kelas konjugasi untuk bentuk siklus ini (Scott 1987, §11.1, p299).

Contoh:

• Kedua permutasi ${\displaystyle (123)}$ dan ${\displaystyle (132)}$ tidak sekawan dalam ${\displaystyle \mathrm {A} _{3}}$, meskipun mereka memiliki bentuk siklus yang sama, dan oleh karena itu sekawan di ${\displaystyle \mathrm {S} _{3}}$ .
• Permutasi (123) (45678) tidak sekawan dengan kebalikannya ${\displaystyle (132)(48765)}$ pada ${\displaystyle \mathrm {A} _{8}}$, meskipun kedua permutasi tersebut memiliki bentuk siklus yang sama, sehingga keduanya sekawan dalam ${\displaystyle \mathrm {S} _{8}}$.

Hubungan dengan grup simetrik

Lihat Grup simetris.

Pembangkit dan relasi

${\displaystyle \mathrm {A} _{n}}$ dihasilkan oleh siklus-3, karena siklus-3 dapat diperoleh dengan menggabungkan pasangan transposisi. Himpunan pembangkit ini sering digunakan untuk membuktikan bahwa ${\displaystyle \mathrm {A} _{n}}$ adalah sederhana untuk ${\displaystyle n\geq 5}$.

Grup automorfisme

${\displaystyle n}$	${\displaystyle \operatorname {Aut} (\mathrm {A} _{n})}$	${\displaystyle \operatorname {Out} (\mathrm {A} _{n})}$
${\displaystyle n\geq 4,n\neq 6}$	${\displaystyle \mathrm {S} _{n}}$	${\displaystyle \mathrm {Z} _{2}}$
${\displaystyle n=1,2}$	${\displaystyle \mathrm {Z} _{1}}$	${\displaystyle \mathrm {Z} _{1}}$
${\displaystyle n=3}$	${\displaystyle \mathrm {Z} _{2}}$	${\displaystyle \mathrm {Z} _{2}}$
${\displaystyle n=6}$	${\displaystyle \mathrm {S} _{6}\rtimes \mathrm {Z} _{2}}$	${\displaystyle \mathrm {V} =\mathrm {Z} _{2}\times \mathrm {Z} _{2}}$

Untuk ${\displaystyle n>3}$, kecuali untuk ${\displaystyle n=6}$, grup automorfisme dari ${\displaystyle \mathrm {A} _{n}}$ adalah grup simetris ${\displaystyle \mathrm {S} _{n}}$, dengan grup automorfisme dalam ${\displaystyle \mathrm {A} _{n}}$ dan grup automorfisme luar ${\displaystyle \mathrm {Z} _{n}}$; automorfisme luar berasal dari konjugasi oleh permutasi ganjil.

Untuk ${\displaystyle n=1}$ dan ${\displaystyle n=2}$, grup automorfisme adalah trivial. Untuk ${\displaystyle n=3}$ grup automorfisme adalah ${\displaystyle \mathrm {Z} _{2}}$, dengan grup automorfisme dalam dan grup automorfisme luar trivial ${\displaystyle \mathrm {Z} _{2}}$.

Grup automorfisme luar ${\displaystyle \mathrm {A} _{6}}$ adalah grup empat Klein ${\displaystyle V=\mathrm {Z} _{2}\times \mathrm {Z} _{2}}$, dan terkait dengan automorfisme luar ${\displaystyle \mathrm {S} _{6}}$. Automorfisme luar ekstra di ${\displaystyle \mathrm {A} _{6}}$ menukar siklus-3 (seperti ${\displaystyle (123)}$) dengan elemen bentuk ${\displaystyle 3^{2}}$ (seperti ${\displaystyle (123)(456)}$).

Isomorfisme istimewa

Terdapat beberapa isomorfisme istimewa antara beberapa grup kecil bergantian dan grup tipe Lie kecil, khususnya grup linear khusus proyektif. Ini adalah:

• ${\displaystyle \mathrm {A} _{4}}$ isomorfik untuk ${\displaystyle \operatorname {PSL} _{2}(3)}$^[1] and grup simetrik
• dari simetri tetrahedrai kiral
• ${\displaystyle \mathrm {A} _{5}}$ isomorfik untuk ${\displaystyle \operatorname {PSL} _{2}(4)}$, ${\displaystyle \operatorname {PSL} _{2}(5)}$, dan kelompok simetri kiral simetri ikosahedral. (Lihat^[1] untuk isomorfisme taklangsung dari ${\displaystyle \operatorname {PSL} _{2}(\mathrm {F} _{5})\to \mathrm {A} _{5}}$ menggunakan klasifikasi grup sederhana berorde 60, dan di sini untuk bukti langsung).
• ${\displaystyle \mathrm {A} _{6}}$ isomorfik untuk ${\displaystyle \operatorname {PSL} _{2}(9)}$ dan ${\displaystyle \operatorname {PSp} _{4}(2)^{\prime }}$.
• ${\displaystyle \mathrm {A} _{8}}$ isomorfik untuk ${\displaystyle \operatorname {PSL} _{4}(2)}$.

Lebih jelasnya, ${\displaystyle \mathrm {A} _{3}}$ isomorfik bagi grup siklik ${\displaystyle \mathrm {Z} _{3}}$, dan ${\displaystyle \mathrm {A} _{0}}$, ${\displaystyle \mathrm {A} _{1}}$, dan ${\displaystyle \mathrm {A} _{2}}$ isomorfik ke grup trivial (yang juga ${\displaystyle \operatorname {SL} _{1}(q)=\operatorname {PSL} _{1}(q)}$ untuk ${\displaystyle q}$).

Contoh ${\displaystyle \mathrm {S} _{4}}$ dan ${\displaystyle \mathrm {A} _{4}}$

Grafik siklus

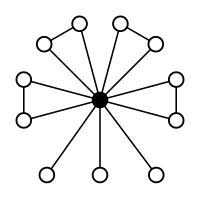${\displaystyle \mathrm {A} _{3}=\mathrm {Z} _{3}}$ (urutan 3)	${\displaystyle \mathrm {A} _{4}}$ (urutan 12)	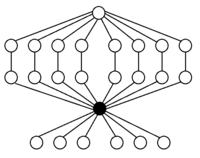${\displaystyle \mathrm {A} _{4}\times \mathrm {Z} _{2}}$ (urutan 24)
${\displaystyle \mathrm {S} _{3}=\operatorname {Dih} _{3}}$ (urutan 6)	${\displaystyle \mathrm {S} _{4}}$ (urutan 24)	${\displaystyle \mathrm {A} _{4}}$ di ${\displaystyle \mathrm {S} _{4}}$ di kiri

Contoh ${\displaystyle \mathrm {A} _{5}}$ sebagai subgrup rotasi ruang-3

${\displaystyle \mathrm {A} _{5}}$ adalah grup isometri dodekahedron dalam 3 ruang, jadi ada wakilan ${\displaystyle \mathrm {A} _{5}\to \operatorname {SO} _{3}(\mathbb {R} )}$

Dalam gambar ini verteks polihedra mewakili elemen grup, dengan pusat bola mewakili elemen identitas. Setiap verteks mewakili rotasi pada sumbu yang menunjuk dari pusat ke verteks tersebut, dengan sudut yang sama dengan jarak dari titik asal, dalam radian. Verteks dalam polihedron yang sama berada dalam kelas sekawan yang sama. Karena persamaan kelas sekawan untuk ${\displaystyle \mathrm {A} _{5}}$ adalah ${\displaystyle 1+12+12+15+20=60}$, kita mendapatkan empat polihedra (taktrivial) berbeda.

Simpul dari setiap polihedron berada dalam korespondensi bijektif dengan elemen kelas sekawannya, dengan pengecualian kelas sekawan siklus-${\displaystyle (2,2)}$, yang diwakili oleh sebuah ikosidodekahedron di permukaan luar, dengan verteks antipodal yang diidentifikasi satu sama lain. Alasan redundansi ini adalah bahwa rotasi terkait oleh ${\displaystyle \pi }$ radian, sehingga dapat diwakili oleh vektor dengan panjang ${\displaystyle \pi }$ di salah satu dari dua arah. Jadi kelas dari siklus-${\displaystyle (2,2)}$ mengandung 15 elemen, sedangkan ikosidodekahedron memiliki 30 verteks.

Dua kelas sekawan dari dua belas siklus-5 dalam ${\displaystyle \mathrm {A} _{5}}$ diwakili oleh dua ikosahedra, dari jari-jari berturut-turut, ${\displaystyle {\frac {2\pi }{5}}}$ dan ${\displaystyle {\frac {4\pi }{5}}}$. Automorfisme luar taktrivial pada ${\displaystyle \operatorname {Out} (\mathrm {A} _{5})\simeq \mathrm {Z} _{2}}$ mempertukarkan kedua kelas ini dan ikosahedra berpadanan.

Catatan

Referensi

Pranala luar

• Weisstein, Eric W. "Alternating group". MathWorld. 
• Weisstein, Eric W. "Alternating group graph". MathWorld.