Cricca (teoria dei grafi)
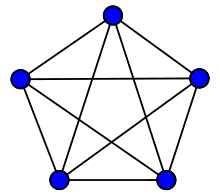
In teoria dei grafi, una cricca (o clique) è un insieme V di vertici in un grafo non orientato G, tale che, per ogni coppia di vertici in V, esiste un arco che li collega. In modo equivalente, si potrebbe dire che il sottografo indotto da V è un grafo completo. La dimensione di una cricca è definita come il numero di vertici che contiene. Alcuni autori chiamano cricca ogni sottografo completo che sia di dimensione massima[1].
Il problema di trovare, se esiste, una cricca di una dimensione fissata all'interno di un grafo è detto problema della cricca, ed è NP-completo.
Il concetto complementare a quello di cricca è l'insieme indipendente, nel senso che a ogni cricca corrisponde un insieme indipendente nel grafo complemento.
Sebbene lo studio dei sottografi completi risalga almeno alla riformulazione della teoria dei grafi con la teoria di Ramsey da parte di Erdős & Szekeres (1935),[2] il termine "cricca" viene da Luce & Perry (1949), che utilizzarono sottografi completi nelle reti sociali per modellare le cricche (in inglese cliques) di persone, vale a dire gruppi ristretti di persone che si conoscono tutte fra di loro. Le cricche hanno molte applicazioni nelle scienze e particolarmente in bioinformatica.
Definizioni
Una cricca in un grafo indiretto G = (V, E) è un sottoinsieme dell'insieme dei vertici C ⊆ V, tale che per ogni due vertici in C, esiste uno spigolo che li connette. Questo equivale a dire che il sottografo indotto da C è completo (in alcuni casi, il termine cricca si può anche riferire al sottografo).
Una cricca massimale è una cricca che non può essere estesa includendo un altro vertice adiacente, cioè una cricca che non esiste esclusivamente dentro l'insieme dei vertici di una cricca più grande.
Una cricca massima è una cricca della dimensione più grande possibile in un dato grafo. Il numero di cricca ω(G) di un grafo G è il numero di vertici in una cricca massima in G. Il numero d'intersezione di G è il più piccolo numero di cricche che insieme coprono tutti gli spigoli di G.
L'opposto di una cricca è un insieme indipendente, nel senso che ogni cricca corrisponde a un insieme indipendente nel grafo complemento. Il problema di copertura delle cricche riguarda il trovare quante più cricche possibile che includano ogni vertice nel grafo. Un concetto correlato è una bicricca (biclique in inglese), un sottografo bipartito completo. La dimensione bipartita di un grafo è il numero minimo di bicricche necessario per coprire tutti gli spigoli del grafo.
Matematica
I risultati matematici concernenti le cricche comprendono i seguenti.
- Il teorema di Turán (1941) dà un limite inferiore alla dimensione di una cricca nei grafi densi. Se un grafo ha un numero sufficientemente alto di spigoli, deve contenere una grande cricca. Ad esempio, ogni grafo con vertici e più di spigoli deve contenere una cricca con tre vertici.
- Il teorema di Ramsey Graham, Rothschild & Spencer (1990) afferma che ogni grafo o il suo grafo complemento contiene una cricca con almeno un numero logaritmico di vertici.
- Secondo un risultato di Moon & Moser (1965), un grafo con 3n vertici può avere al massimo 3n cricche massimali. I grafi che incontrano questo limite sono i grafi di Moon–Moser K3,3,..., un caso speciale dei grafi di Turán che emergono come i casi estremali del teorema di Turán.
- La congettura di Hadwiger, ancora non dimostrata, collega la dimensione della più grande cricca di un minore in un grafo (il suo numero di Hadwiger) al suo numero cromatico.
- La congettura di Erdős–Faber–Lovász è un'altra affermazione non dimostrata che collega la colorazione dei grafi alle cricche.
Varie importanti classi di grafi possono essere definiti dalle loro cricche:
- Un grafo cordale è un grafo i cui vertici possono essere ordinati in un perfetto ordinamento di eliminazione, un ordinamento tale che i vicini di ciascun vertice v che vengono dopo v nell'ordinamento formano una cricca.
- Un cografo è un grafo i cui sottografi indotti hanno tutti la proprietà che qualsiasi cricca massimale interseca qualsiasi insieme indipendente massimale in un unico vertice.
- Un grafo d'intervallo è un grafo le cui cricche massimali possono essere ordinate in modo tale che, per ciascun vertice v, le cricche contenenti v sono consecutive nell'ordinamento.
- Un grafo di linea è un grafo i cui spigoli possono essere coperti da cricche con gli spigoli disgiunti in modo tale che ogni vertice appartiene esattamente a due delle cricche nella copertura.
- Un grafo perfetto è un grafo nel quale il numero di cricca equivale al numero cromatico in ogni sottografo indotto.
- Un grafo diviso è un grafo nel quale alcune cricche contengono almeno un estremo di ogni spigolo.
- Un grafo senza triangoli è un grafo che non ha cricche distinte dai suoi vertici e dai suoi spigoli.
In aggiunta, molte altre costruzioni matematiche coinvolgono le cricche dei grafi. Tra di esse:
- Il complesso delle cricche di un grafo G è un complesso simpliciale astratto X(G) cvon un simplesso per ogni cricca in G
- Un grafo semplice è un grafo indiretto κ(G) con un vertice per ogni cricca in un grafo G e uno spigolo che connette due cricche che differiscono per un singolo vertice. È un esempio di grafo mediano, ed è associato a un'algebra mediana sulle cricche di un grafo: la mediana m(A,B,C) di tre cricche A, B e C è la cricca i cui vertici appartengono ad almeno due delle cricche A, B e C.[3]
- La somma delle cricche è un metodo per combinare due grafi fondendoli lungo una cricca condivisa.
- L'ampiezza di cricca è una nozione della complessità di un grafo in termini del numero minimo di distinte etichette dei vertici necessarie per costruire il grafo a partire dalle unioni disgiunte, dalle operazioni di rietichettamento e dalle operazioni che connettono tutte le coppie di vertici con etichette date. I grafi con ampiezza di cricca uno sono esattamente le unioni disgiunte delle cricche.
- Il numero d'intersezione di un grafo è il numero minimo di cricche necessarie per coprire tutti gli spigoli del grafo.
Concetti strettamente correlati ai sottografi completi sono le suddivisioni dei grafi completi e dei minori completi dei grafi. In particolare, il teorema di Kuratowski e il teorema di Wagner caratterizzano i grafi planari rispettivamente mediante le suddivisioni e i minori completi proibiti e bipartiti completi.
Informatica
In informatica, il problema della cricca è il problema computazionale di trovare una cricca massima, o tutte le cricche, in un dato grafo. È NP-completo, uno dei 21 problemi NP-completi di Karp (M. Richard Karp, 1972). È anche intrattabile con parametri fissi, e difficile da approssimare. Nondimeno, sono stati sviluppati molti algoritmi per computare le cricche, o funzionanti in tempo esponenziale (come l'algoritmo di Bron-Kerbosch) o specializzati in famiglie di grafi come i grafi planari o grafi perfetti per i quali il problema possa essere risolto in tempo polinomiale.
Programmi liberi per la ricerca della massima cricca
| Nome | Licenza | Linguaggio API | Breve info |
|---|---|---|---|
| NetworkX | BSD | Python | soluzione approssimata, vedi la routine max_clique[4] |
| maxClique | CRAPL | Java | algoritmi esatti e istanze DIMACS |
| OpenOpt | BSD | Python | soluzioni esatte e approssimate, possibilità di specificare i nodi che devono essere inclusi / esclusi; vedi la classe MCP Archiviato il 3 ottobre 2013 in Internet Archive. per maggiori dettagli ed esempi |
Applicazioni
La parola "cricca", nel suo uso nella teoria dei grafi, emerse dal lavoro di Luce & Perry (1949), che utilizzarono sottografi per modellare le cricche (gruppi di persone che si conoscono tutte fra di loro) nelle reti sociali. Per la continuazione dei tentativi di modellare le cricche sociali dal punto di vista della teoria dei grafi, vedi ad es. Alba (1973), Peay (1974), e Doreian & Woodard (1994).
Molti diversi problemi di bioinformatica sono stati modellati usando le cricche. Ad esempio, Ben-Dor, Shamir & Yakhini (1999) modellano il problema di raggruppare i dati sull'espressione genica come quello di trovare il numero minimo di cambiamenti necessari per trasformare un grafo che descrive i dati in un grafo formato come l'unione disgiunta delle cricche; Tanay, Sharan & Shamir (2002) discutono un problema simile di biraggruppamento per dati sull'espressione in cui si richiede che i gruppi siano cricche. Sugihara (1984) usa le cricche per modellare le nicchie ecologiche nelle reti alimentari. Sankoff descrive il problema di inferire gli alberi evolutivi come quello di trovare le massime cricche in un grafo che ha come suoi vertici le caratteristiche della specie, dove due vertici condividono uno spigolo se esiste una perfetta filogenia che combina quei due caratteri. Samudrala & Moult (1998) modellano la predizione di struttura proteica come un problema di trovare le cricche in un grafo i cui vertici rappresentano posizioni di sottounità nella proteina. E cercando le cricche in una rete d'interazione proteina-proteina, Spiron & Mirny (2003) trovarono raggruppamenti di proteine che interagiscono strettamente tra loro e hanno poche interazioni con le proteine al di fuori del raggruppamento. L'analisi dei grafi di potenza è un metodo per semplificare le reti biologiche complesse trovando le cricche e le strutture relative in queste reti.
In ingegneria elettrica, Prihar (1956) usa le cricche per analizzare le reti di comunicazione, e Paull, 1959 le usano per progettare circuiti efficienti per computare funzioni booleane parzialmente specificate. Le cricche sono state usate anche nella generazione di programmi di prova automatici: una grande cricca in un grafo d'incompatibilità di possibili guasti fornisce un limite inferiore sulla dimensione di un insieme di prove.[5] Cong1993, Cong & Smith (1993) descrivono un'applicazione delle cricche per trovare una partizione gerarchica di un circuito elettronico in sottounità più piccole.
In chimica, Rhodes, Willett, Calvet & Dunbar (2003) usano le cricche per descrivere le sostanze chimiche in una base di dati chimica che hanno un alto grado di similarità con una struttura bersaglio. Kuhl, Crippen & Friesen (1983) usano le cricche per modellare le posizioni in cui due sostanze chimiche si legheranno l'una all'altra.
Note
- ^ Harary, F. Graph Theory. Reading, MA: Addison-Wesley, 1994
- ^ Il lavoro anteriore di Kuratowski, che caratterizzava i grafi planari mediante sottografi completi e bipartiti completi di tipo vietato, era formulato originariamente in termini topologici piuttosto che grafo-teorici.
- ^ Barthélemy, Leclerc & Monjardet (1986), p. 200.
- ^ (EN) max_clique, su networkx.lanl.gov. URL consultato il 26 maggio 2022 (archiviato dall'url originale il 24 luglio 2013).
- ^ Hamzaoglu & Patel (1998).
Bibliografia
- Richard D. Alba, A graph-theoretic definition of a sociometric clique (PDF), in Rivista of Mathematical Sociology, vol. 3, n. 1, 1973, 113–126, DOI:10.1080/0022250X.1973.9989826. URL consultato il 25 marzo 2014 (archiviato dall'url originale il 3 maggio 2011).
- J.-P. Barthélemy, B. Leclerc e B. Monjardet, On the use of ordered sets in problems of comparison and consensus of classifications, in Rivista of Classification, vol. 3, n. 2, 1986, 187–224, DOI:10.1007/BF01894188.
- Amir Ben-Dor, Ron Shamir e Zohar Yakhini, Clustering gene expression patterns., in Rivista of Computational Biology, vol. 6, 3–4, 1999, 281–297, DOI:10.1089/106652799318274, PMID 10582567.
- Cong J. e Smith M., A parallel bottom-up clustering algorithm with applications to circuit partitioning in VLSI design, in Proc. 30th International Design Automation Conference, 1993, 755–760, DOI:10.1145/157485.165119.
- William H. E. Day e David Sankoff, Computational complexity of inferring phylogenies by compatibility, in Systematic Zoology, vol. 35, n. 2, 1986, 224–229, DOI:10.2307/2413432, JSTOR 2413432.
- Patrick Doreian e Katherine L. Woodard, Defining and locating cores and boundaries of social networks, in Social Networks, vol. 16, n. 4, 1994, 267–293, DOI:10.1016/0378-8733(94)90013-2.
- Paul Erdős e George Szekeres, A combinatorial problem in geometry (PDF), in Compositio Math., vol. 2, 1935, 463–470.
- R. Graham, B. Rothschild e J. H. Spencer, Ramsey Theory, New York, John Wiley and Sons, 1990, ISBN 0-471-50046-1.
- I. Hamzaoglu e J. H. Patel, Test set compaction algorithms for combinational circuits, in Proc. 1998 IEEE/ACM International Conference on Computer-Aided Design, 1998, 283–289, DOI:10.1145/288548.288615.
- Richard M. Karp, Reducibility among combinatorial problems (PDF), in R. E. Miller e J. W. Thatcher (a cura di), Complexity of Computer Computations, New York: Plenum, 1972, 85–103. URL consultato il 30 aprile 2019 (archiviato dall'url originale il 4 marzo 2016).
- F. S. Kuhl, G. M. Crippen e D. K. Friesen, A combinatorial algorithm for calculating ligand binding, in Rivista of Computational Chemistry, vol. 5, n. 1, 1983, 24–34, DOI:10.1002/jcc.540050105.
- (FR) Kazimierz Kuratowski, Sur le probléme des courbes gauches en Topologie (PDF), in Fundamenta Mathematicae, vol. 15, 1930, 271–283.
- R. Duncan Luce e Albert D. Perry, A method of matrix analysis of group structure, in Psychometrika, vol. 14, n. 2, 1949, 95–116, DOI:10.1007/BF02289146, PMID 18152948.
- J. W. Moon e L. Moser, On cliques in graphs, in Israel J. Math., vol. 3, 1965, 23–28, DOI:10.1007/BF02760024, MR 0182577.
- M. C. Paull e S. H. Unger, Minimizing the number of states in incompletely specified sequential switching functions, in IRE Trans. on Electronic Computers, EC-8, n. 3, 1959, 356–367, DOI:10.1109/TEC.1959.5222697.
- Edmund R. Peay, Hierarchical clique structures, in Sociometry, vol. 37, n. 1, 1974, 54–65, DOI:10.2307/2786466, JSTOR 2786466.
- Z. Prihar, Topological properties of telecommunications networks, in Proceedings of the IRE, vol. 44, n. 7, 1956, 927–933, DOI:10.1109/JRPROC.1956.275149.
- Nicholas Rhodes, Peter Willett, Alain Calvet, James B. Dunbar e Christine Humblet, CLIP: similarity searching of 3D databases using clique detection, in Rivista of Chemical Information and Computer Sciences, vol. 43, n. 2, 2003, 443–448, DOI:10.1021/ci025605o, PMID 12653507.
- Ram Samudrala e John Moult, A graph-theoretic algorithm for comparative modeling of protein structure, in Rivista of Molecular Biology, vol. 279, n. 1, 1998, 287–302, DOI:10.1006/jmbi.1998.1689, PMID 9636717.
- Victor Spirin e Leonid A. Mirny, Protein complexes and functional modules in molecular networks, in Proceedings of the National Academy of Sciences, vol. 100, n. 21, 2003, 12123–12128, DOI:10.1073/pnas.2032324100, PMC 218723, PMID 14517352.
- George Sugihara, Graph theory, homology and food webs, in Simon A. Levin (a cura di), Population Biology, Proc. Symp. Appl. Math., vol. 30, 1984, 83–101.
- Amos Tanay, Roded Sharan e Ron Shamir, Discovering statistically significant biclusters in gene expression data, in Bioinformatics, vol. 18, Suppl. 1, 2002, S136–S144, DOI:10.1093/bioinformatics/18.suppl_1.S136, PMID 12169541.
- (HU) Paul Turán, On an extremal problem in graph theory, in Matematikai és Fizikai Lapok, vol. 48, 1941, 436–452.
Voci correlate
- Problema della cricca
- Insieme indipendente (teoria dei grafi)
Collegamenti esterni
- (EN) Eric W. Weisstein, Cricca, su MathWorld, Wolfram Research.

 Portale Informatica
Portale Informatica Portale Matematica
Portale Matematica












