ウィンドケッセルモデル

ウィンドケッセルモデル（英: Windkessel model）とは、医学、特に循環生理学において動脈圧の波形を一回拍出量と動脈壁のコンプライアンスの相互作用の観点から説明する際に使われる概念である。

"Windkessel" は元はドイツ語であり、英語に直訳すれば "air chamber" 、即ち「空気室」となるが^[1][2]、通常は「弾性を持った貯留槽モデル」といったニュアンスで使用される^[3]。太い弾性血管（例： 大動脈、総頸動脈、鎖骨下動脈、肺動脈、そしてそれらの主要分枝）はエラスチンによって構成された弾性線維を含んでいる。これらの血管は収縮期に血圧が上がると拡張し、拡張期に血圧が下がるともとの径に収縮する。末梢血管抵抗（英語版）があるために、それらの弾性血管に流入する血流量は、流出する血流量よりも多くなる。そのため、収縮期に差し引きの血液量が血管内に蓄えられ、それが拡張期に末梢側に放出されることになる。その結果、心臓からの血液の拍出が止まる拡張期でも臓器への血液灌流が維持されている。これをウィンドケッセル効果（Windkessel effect）と呼ぶ。ウィンドケッセル効果は、一回の心周期（英語版）における血圧の変動（＝脈圧）に対する緩衝作用を果たしている。

ウィンドケッセルの概念は当初ジョバンニ・ボレリにより示唆されたものであるが、更にスティーヴン・ヘールズにより概念が整理・明瞭化され、18世紀当時の消防ポンプで使用されていた空気室とのアナロジーを用いて説明された（上図のイラスト参照）^[4]。その後ドイツの生理学者オットー・フランク（Otto Frank）により、厳密な数学的基礎のもとに定式化された^[2]。フランクのモデルは後述する「2要素ウィンドケッセルモデル」に相当し、後に拡張されたより複雑なモデル（3要素・4要素ウィンドケッセル）とは区別されることがある^[5]。

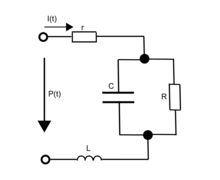
ウィンドケッセルモデルにおいて、太い弾性血管の伸展性は電気回路との対比においてキャパシタに相当すると言える。電気回路に模したモデルのうち、2要素・3要素・4要素の等価回路を右の図に示す^[6]。

最も単純な血行動態を表すモデルは2要素モデルであり、動脈コンプライアンスと全末梢血管抵抗の影響を考慮したものである。

右図の等価回路では、動脈コンプライアンスを電荷を蓄えるキャパシタの容量 C に、体循環の末梢血管抵抗を抵抗器の抵抗 R に対応させている。心臓から拍出される血液量は電流に対応し I(t) として、また大動脈の血圧は電位 P(t) としてそれぞれ時間の関数で表されている。

この時電流（心拍出量）、電位（大動脈圧）の関係は、以下の微分方程式として表される。

${\displaystyle I(t)={\frac {P(t)}{R}}+C{\frac {dP(t)}{dt}}}$

2要素モデルの解析の一例として、ここでは心室から大動脈に流出する血流を正弦波でシミュレートする。また単純化のために、等容収縮時間（英語版）と等容弛緩時間を無視する。即ち収縮期の開始と同時に大動脈弁の開放が起こり、大動脈弁の閉鎖と同時に拡張期に入ると仮定する。

振幅を I₀、心周期時間を T_c、収縮期時間を T_sで表すと、収縮期の血流は

${\displaystyle I(t)=I_{0}\ \mathrm {sin} \left(\pi \cdot {\frac {t\ \mathrm {mod} \ T_{c}}{T_{s}}}\right)}$

となる。ここで mod は mod演算子（mod operator）である。I₀ と一回拍出量（Stroke Volume）は比例し、両者には

${\displaystyle Stroke\ Volume=\int _{0}^{T_{s}}I(t)\,dt={\frac {2I_{0}T_{s}}{\pi }}}$

の関係がある。また拡張期に拍出される血流は

${\displaystyle I(t)=0}$

となる（ここでは大動脈弁閉鎖不全症などは無い理想的な状況を想定していることに注意）。

実際にこのモデルを解析的に解くと、まず 0 ≤ t ≤ T_s の収縮期では

${\displaystyle P(t)=c_{1}e^{\frac {-t}{CR}}-{\frac {I_{0}T_{s}R\left(\pi CR\mathrm {cos} \left({\frac {\pi t}{T_{s}}}\right)-T_{s}\mathrm {sin} \left({\frac {\pi t}{T_{s}}}\right)\right)}{T_{s}^{2}+(\pi CR)^{2}}}}$

但し定数 c₁ は、収縮初期の血圧を P_ssとして

${\displaystyle c_{1}=P_{ss}+{\frac {I_{0}T_{s}R(\pi CR)}{T_{s}^{2}+(\pi CR)^{2}}}}$

となる。一方 T_s ≤ t ≤ T_c の拡張期では、

${\displaystyle {\frac {P(t)}{R}}+C{\frac {dP(t)}{dt}}=0}$

となるので

${\displaystyle P(t)=c_{2}e^{\frac {-t}{CR}}}$

即ち指数関数的減衰曲線となり、これがウィンドケッセル効果により拡張期に末梢側に血流を送り出す血圧を表している。定数 c₂ を求めるには拡張初期の血圧 P_sd が必要であるが、P_sd は収縮期における解から求められる収縮末期圧に依存する。この場合は等容弛緩時間を無視しているので、

${\displaystyle P_{sd}=P(T_{s})=P_{ss}e^{\frac {-T_{s}}{CR}}+{\frac {I_{0}T_{s}R(\pi CR)}{T_{s}^{2}+(\pi CR)^{2}}}\left(e^{\frac {-T_{s}}{RC}}+1\right)}$

として求められる P_sd を用いて、

${\displaystyle c_{2}=P_{sd}e^{\frac {T_{s}}{CR}}=P_{ss}+{\frac {I_{0}T_{s}R(\pi CR)}{T_{s}^{2}+(\pi CR)^{2}}}\left(1+e^{\frac {T_{s}}{CR}}\right)}$

となる。上記の結果から収縮期・拡張期いずれにおいても、一回拍出量に相関する I₀ と動脈コンプライアンス C 、また末梢血管抵抗を表す R が動脈圧波形に関与することが分かる。

3要素モデルでは、更に大動脈基部の特性インピーダンスを考慮に入れる。大動脈弁による抵抗を説明するため、上述の2要素モデルに抵抗 r を追加する。心臓から拍出される血流に対する抵抗は大動脈弁の開閉により変動する。このモデルは以下の微分方程式で表される。

${\displaystyle \left(1+{\frac {r}{R}}\right)I(t)+rC{\frac {dI(t)}{dt}}={\frac {P(t)}{R}}+C{\frac {dP(t)}{dt}}}$

4要素モデルでは、血流の慣性を表現するためにインダクタを導入する。インダクタでの電位の降下は L(dI(t)/dt) で表す。4要素モデルは心周期に伴う血行動態を2要素・3要素モデルより更に正確にモデル化することが出来る。

${\displaystyle \left(1+{\frac {r}{R}}\right)I(t)+\left(rC+{\frac {L}{R}}\right){\frac {dI(t)}{dt}}+LC{\frac {d^{2}I(t)}{dt^{2}}}={\frac {P(t)}{R}}+C{\frac {dP(t)}{dt}}}$

加齢が進むと動脈壁硬化により弾性血管のコンプライアンスが低下するため、ウィンドケッセル効果は減少する。原因は弾性繊維のエラスチンの分解・喪失が関与していると思われる。ウィンドケッセル効果の減少は脈圧を増大させるため、一回拍出量が一定の条件のもとでは収縮期血圧を上昇させる。収縮期血圧の上昇、即ち高血圧は、心筋梗塞、脳血管障害、心不全、その他様々な心血管疾患の危険因子となる^[7]。

ウィンドケッセルモデルの応用として、適切なモデルを設定し圧波形を解析することにより要素ごとのパラメーターを求め、血管床の生理学的特性を明らかにする研究が行われている。

一例として、左右シャントを伴う先天性心疾患では肺高血圧クライシスを起こす可能性があるため肺血管床の評価をする必要があるが、肺動脈圧波形の解析から得られる肺動脈コンプライアンスなどの指標の有用性が検討されている^[8]。

具体的には、上記の2要素モデルの結果を肺動脈に応用することにより、拡張期の肺動脈圧波形が指数関数的減衰曲線になると仮定する。拡張期のある時刻 t₁、t₂ （t₁＜t₂）における肺動脈圧をそれぞれ P₁、P₂ とすると、拡張期時定数（diastolic time constant）T_d は

${\displaystyle T_{d}=-{\frac {t_{2}-t_{1}}{\mathrm {ln} \left(P_{2}/P_{1}\right)}}}$

また平均肺動脈圧をmPAP 、平均左房圧（または肺動脈楔入圧）をmLAP 、肺血流量をQ_pとすると、肺血管抵抗R_pは

${\displaystyle R_{p}={\frac {mPAP-mLAP}{Q_{p}}}}$

として与えられる。肺動脈カテーテルを用いてこれらの値を実際に計測し、肺動脈の拡張期コンプライアンスC_dを

${\displaystyle C_{d}={\frac {T_{d}}{R_{p}}}}$

として求めることが出来る。また左房圧を基準とした収縮期・拡張期・平均肺動脈圧とC_dから、肺血管床を

${\displaystyle WS_{s}=(maximum\ systolic\ PAP-mLAP)\cdot C_{d}}$

${\displaystyle WS_{d}=(minimum\ diastolic\ PAP-mLAP)\cdot C_{d}}$

${\displaystyle WS_{m}=(mPAP-mLAP)\cdot C_{d}}$

として計算出来る。WS_s、WS_d、WS_mをそれぞれ収縮期・拡張期・平均のウィンドケッセル容積（Windkessel size）と呼ぶ。

ウィンドケッセルモデルはその単純さから循環動態を考察するのに便利なモデルであるが、あくまで脈管系を巨視的に見たもので、血流や圧伝播の局所的な詳細を論じる事はできない。動脈圧とその波形の解釈に対するより現代的なアプローチとしては脈波伝播と反射波による脈波伝播モデル（propagation model）があり、広く使われつつある^[9][10]。一方、脈波伝播モデルとウィンドケッセルモデルとの統合を試みるアプローチも存在する^[11]。

• 血流
• 血圧
• 動脈
• 弾性
• コンプライアンス
• 動脈スティフネス
• 先天性心疾患