単射的対象

数学，特に圏論において，単射的対象（たんしゃてきたいしょう，英: injective object, あるいは移入的対象，入射的対象）の概念は単射的加群の概念の一般化である．この概念はホモトピー論とモデル圏の理論において重要である．双対概念は射影的対象である．

定義

Q が H 単射的とは，H における射 A → B が与えられたとき，任意の A → Q が B → Q に拡張することをいう．

${\mathfrak {C}}$ を圏とし ${\mathcal {H}}$ を ${\mathfrak {C}}$ の射のあるクラスとする．

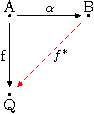
${\mathfrak {C}}$ の対象 Q が ${\mathcal {H}}$ -単射的とは， ${\mathcal {H}}$ の任意の射 f: A → Q と任意の射 h: A → B に対して，ある射 g: B → Q が存在して f （の始域）を拡張する，すなわち $g\circ h=f$ となることをいう．

上の定義における射 g は h と f によって一意的に決定されることは要求されない．

局所的に小さい圏では，それはhom関手 $Hom_{\mathfrak {C}}(-,Q)$ が ${\mathcal {H}}$ -射を全射に送ることと同値である．

${\mathcal {H}}$ の古典的な選択は単射全体のクラスであり，この場合，単射的対象という表現が使われる．

アーベル圏の場合

アーベル圏の場合が単射性の概念のもともとの枠組みであった（そして今でも最も重要なものである）． ${\mathfrak {C}}$ がアーベル圏のとき， ${\mathfrak {C}}$ の対象 A が単射的であるとは，hom関手 Hom_C(–,A) が完全であることをいう．

0\to A\to B\to C\to 0

を ${\mathfrak {C}}$ における完全列であって A が単射的対象であるものとする．すると列は分裂し，B が単射的であることと C が単射的であることは同値である^[1]．

充分単射的対象をもつ

${\mathfrak {C}}$ を圏とし，H を ${\mathfrak {C}}$ の射のあるクラスとする；圏 ${\mathfrak {C}}$ が充分 H 単射的対象をもつ (have enough H injectives) とは， ${\mathfrak {C}}$ のすべての対象 X に対して，X からある H-単射的対象へのある H 射が存在することをいう．

単射的包絡

${\mathfrak {C}}$ における H 射 g が H 本質的 (H-essential) であるとは，任意の射 f に対して，合成 fg が H に属するのは f が H に属するときに限ることをいう．H が単射全体のクラスであるとき，g は本質的単射（英語版）と呼ばれる．

f が H 本質的 H 射であって，始域が X, 余域が H 単射的な G であるとき，G は X の H 単射的包絡 (H-injective hull) と呼ばれる．するとこの H 単射的包絡は，標準的でない同型の違いを除いて一意的である．

例

アーベル群と群準同型の圏において，単射的対象は可除群である．
加群と加群準同型の圏 R-Mod において，単射的対象は単射的加群である．R-Mod は単射的包絡をもつ（したがって R-Mod は充分単射的対象をもつ）．
距離空間とnonexpansive mapping（英語版）の圏 Met において，単射的対象は超凸距離空間（英語版）であり，距離空間の単射的包絡はその超凸包（英語版）である．
T₀ 空間と連続写像の圏において，単射的対象は必ず連続束上のスコット位相であり，したがってそれは必ずsober（英語版）かつ局所コンパクトである．
単体的集合（英語版）の圏において，anodyne extensions のクラスに関する単射的対象はカン複体（英語版）である．
半順序集合と単調写像の圏において，完備束は順序埋め込み（英語版）に対する単射的対象をなし，半順序集合の Dedekind–MacNeille 完備化（英語版）はその単射的包絡である．
より一般の圏，例えば関手圏や，環付き空間 (X, O_X) 上の O_X 加群の層の圏においても単射的対象を考えることができる．