Bézout teoremi

Bézout teoremi, cebirsel geometride n değişkenli n polinomun ortak sıfırlarının sayısı ile ilgili bir ifadedir. Orijinal biçiminde teorem, genel olarak ortak sıfırların sayısının, polinomların derecelerinin çarpımına eşit olduğunu belirtir. Adını Fransız matematikçi Étienne Bézout[1][not 1]'dan almıştır.
Bazı temel metinlerde, Bézout'un teoremi yalnızca iki değişken durumuna atıfta bulunur ve ve dereceli iki düzlem cebirsel eğrisinin ortak bir bileşeni yoksa, bunların katlılık sayısı (multiplicity) ile sayılan ve sonsuzdaki noktalar ile karmaşık koordinatlara sahip noktalar dahil kesişim noktasına sahip olduklarını iddia eder.
Modern formülasyonunda teorem şunu belirtir; N, n + 1 değişkenli homojen polinomlarla tanımlanan n izdüşümsel hiper yüzeyin bir cebirsel kapalı cisim üzerindeki ortak noktaların sayısı ise, bu durumda N, sonsuzdur veya polinomların derecelerinin çarpımına eşittir. Dahası, sonlu durum neredeyse her zaman ortaya çıkar.
İki değişkenli durumda ve afin hiper yüzeyleri durumunda, sonsuzdaki katlılık sayıları ve noktalar sayılmazsa, bu teorem, neredeyse her zaman ulaşılan nokta sayısının yalnızca bir üst sınırını sağlar. Bu sınır genellikle Bézout sınırı olarak adlandırılır.
Bézout'un teoremi, çoğu problemin değişken sayısında en azından üstel olan bir hesaplama karmaşıklığına sahip olduğunu göstererek, bilgisayar cebiri ve etkili cebirsel geometride temeldir. Bu alanlarda, Bézout sınırında polinom olan bir karmaşıklığa sahip algoritmalarla umulabilecek en iyi karmaşıklık ortaya çıkacaktır.
Tarihçe
Düzlem eğriler söz konusu olduğunda, Bézout teoremi esasen Isaac Newton tarafından 1687'de Principia'nın 1. cildinin 28. lemmasının ispatında belirtildi, burada iki eğrinin derecelerinin çarpımı tarafından verilen sayıda kesişme noktasına sahip olduğunu iddia etti.
Genel teorem daha sonra 1779'da Étienne Bézout'un Théorie générale des équations algébriques adlı eserinde yayınlandı. O, denklemlerin "tam" olduğunu ve modern terminolojide jenerik olarak çevrilebileceğini düşünüyordu. Jenerik polinomlarda sonsuzda nokta olmadığından ve tüm katlılık sayıları bire eşit olduğundan, Bézout'un formülasyonu doğrudur, ancak kanıtı, kesinliğin modern gereklerini karşılamıyordu.
Bu ve kesişim katlılık sayısı (intersection multiplicity) kavramının zamanının bilgisi dışında olması, bazı yazarlar tarafından ispatının ne doğru ne de verilen ilk ispat olmadığını ifade eden bir algıya yol açtı.[2]
Katlılık sayıları içeren ifadenin ispatı 20. yüzyıldan önce soyut cebir ve cebirsel geometrinin tanıtılmasıyla mümkün değildi.
Açıklama
Düzlem eğriler
X ve Y’nin, ortak bir bileşeni olmayan bir F cismi üzerinde tanımlanan iki düzlemsel izdüşümsel eğri olduğunu varsayalım (bu koşul, X ve Y'nin ortak sabit olmayan bir polinomun katları olmayan polinomlar tarafından tanımlandığı anlamına gelir; özellikle, bir çift "jenerik" eğri için geçerlidir).
Daha sonra, F’yi içeren cebirsel kapalı bir E cismindeki koordinatlarla X ve Y'nin katlılık sayıları ile sayılan kesişme noktalarının toplam sayısı, X ve Y derecelerinin çarpımına eşittir.
Genel durum
Daha yüksek boyuttaki genelleme şu şekilde ifade edilebilir:
N tane izdüşümsel hiper yüzey, dereceli n + 1 değişkende n homojen polinom ile tanımlanan cebirsel olarak kapalı bir cisim üzerinde n boyutundaki bir izdüşümsel uzayda verilsin. O zaman ya kesişim noktalarının sayısı sonsuzdur ya da katlılık sayısı ile sayılan kesişme noktalarının sayısı çarpıma eşittir. Hiper yüzeyler indirgenemezse ve göreceli genel konumdaysa, o zaman hepsinin katlılık sayısı 1 olan kesişme noktası vardır.
Bu teoremin, tamamen cebirsel terimlerle ifade edilen veya dili veya cebirsel geometriyi kullanan çeşitli ispatları vardır. Üç cebirsel ispat aşağıda özetlenmiştir.
Bézout teoremi, çoklu homojen Bézout teoremi olarak genelleştirilmiştir.
Örnekler (düzlem eğriler)
İki doğru
Öklid düzleminde bir doğrunun denklemi doğrusaldır, yani birinci dereceden bir polinomu sıfıra eşittir. Bu nedenle, iki çizgi için Bézout sınırı 1'dir, yani iki doğru ya tek bir noktada kesişir ya da kesişmez. İkinci durumda, çizgiler paraleldir ve sonsuzda bir noktada kesişir.
Bunu denklemlerle doğrulayabilirsiniz. İlk satırın denklemi eğim-kesme noktası biçiminde olarak yazılabilir veya izdüşümsel koordinatlarda olarak yazılabilir (çizgi dikse, x ve y yer değiştirebilir). Eğer ikinci bir doğrunun denklemi (izdüşümsel koordinatlarda) , ise y yerine yazılırsa, elde edilir. Eğer , ise ikinci denklemi x değişkeninde çözülür ve t = 1 alınırsa x-koordinatının kesişme noktası elde edilir.
Eğer yani ise iki çizgi paraleldir ve aynı eğime sahiptir. Eğer ise bunlar farklıdır ve yerine konmuş denklem t = 0 verir. Bu, (1, s, 0) izdüşümsel koordinatların sonsuzdaki noktasını verir.
Bir doğru ve bir eğri
Yukarıdaki gibi, izdüşümsel koordinatlarda doğrunun denklemi: şeklinde yazılabilir. Eğri, izdüşümsel koordinatlarda n dereceden homojen bir polinomu ile tanımlanmışsa, y'nin yerine konması, x ve t türünden n. derece homojen bir polinom sağlar. Cebirin temel teoremi, doğrusal faktörlerde çarpanlarına ayrılabileceğini işaret eder. Her faktör, bir kesişme noktasının x ve t koordinatlarının oranını verir ve çarpanın katlılık sayısı, kesişme noktasının katlılık sayısıdır.
t sonsuz'un koordinatı olarak görülürse, t'ye eşit bir çarpan, sonsuzda bir kesişme noktasını temsil eder.
Polinom p'nin en az bir kısmi türevi, bir kesişme noktasında sıfır değilse, bu noktada eğrinin teğeti tanımlanır (bkz. Cebirsel eğri § Bir noktada teğet), ancak ve sadece doğru eğriye teğet ise kesişim katlılık sayısı birden büyüktür. Tüm kısmi türevler sıfırsa, kesişme noktası tekil bir noktadır ve kesişim katlılık sayısı en az ikidir.
İki konik kesit
İki konik kesit genellikle dört noktada kesişir ve bunlardan bazıları çakışabilir. Tüm kesişme noktalarını doğru bir şekilde hesaba katmak için, karmaşık koordinatlara izin vermek ve izdüşümsel düzlemde sonsuz doğru üzerindeki noktaları dahil etmek gerekli olabilir. Örneğin:
- Bézout'un teoremi dört taneyi tahmin ederken, iki çember düzlemde ikiden fazla noktada kesişmez. Tutarsızlık, her çemberin sonsuzda doğrunun aynı iki karmaşık noktasından geçmesinden kaynaklanır. Çemberi aşağıdaki denklemle yazarsak;
- homojen koordinatlarda,
- buluruz. Burada iki noktanın (1:i:0) ve (1:-i:0), her çemberin üzerinde olduğu açıktır. İki çember, gerçek düzlemde hiç kesişmediğinde, diğer iki kesişimin sıfır olmayan imajiner kısımları vardır veya eşmerkezli iseler, o zaman iki kesişim katlılık sayısı ile sonsuzda doğrunun iki noktasında buluşurlar.
- Teoreme göre herhangi bir konik, iki noktada sonsuzda doğruyla buluşmalıdır. Bir hiperbol, asimptotların iki yönüne karşılık gelen iki gerçek noktada karşılaşır. Bir elips, birbiriyle eşlenik olan iki karmaşık noktada buluşur - bir çember durumunda, noktalar (1 : i : 0) ve (1: -i : 0)'dir. Bir parabol, onunla yalnızca bir noktada karşılaşır, ancak bu bir teğet noktasıdır ve bu nedenle iki kez sayılır.
- Aşağıdaki resimler, x2 + y2 -1 = 0 çemberinin daha az kesişim noktasında başka bir elips ile karşılaştığı örnekleri gösterir, çünkü bunlardan en az biri 1'den büyük katlılık sayısına sahiptir:
-
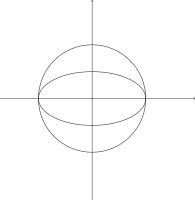 2 katlılık sayısının iki kesişim noktası:
2 katlılık sayısının iki kesişim noktası: -
 3 katlılık sayısının kesişim noktası:
3 katlılık sayısının kesişim noktası: -
 4 katlılık sayısının kesişim noktası:
4 katlılık sayısının kesişim noktası:
Katlılık sayısı (Multiplicity)
Katlılık sayısı kavramı, çok daha zayıf bir eşitsizlik yerine bir eşitliğe sahip olmasına izin verdiği için Bézout teoremi için temeldir.
Sezgisel olarak, birkaç polinomun ortak bir sıfırının katlılık sayısı, katsayılar düşük ihtimalle bölünebileceği sıfırların sayısıdır. Örneğin, bir eğriye teğet, eğriyi bir noktada kesen, doğru hafifçe hareket ettirilirse eğriyi birkaç noktada bölen bir doğrudur. Bu sayı genel olarak ikidir (sıradan noktalar), ancak daha fazla da olabilir (bükülme noktaları için üç, dalgalanma noktaları için dört vb.). Bu sayı, teğetin "temas katlılık sayısı (multiplicity of contact)"dır.
Deformasyon yoluyla katlılık sayılarının bu tanımı, 19. yüzyılın sonuna kadar yeterliydi, ancak daha uygun modern tanımlara yol açan birkaç problemi vardır: Deformasyonların değiştirilmesi zordur; örneğin, bir tek değişkenli polinomun bir kökü durumunda, deformasyonla elde edilen katlılık sayısının, polinomun karşılık gelen doğrusal faktörünün katlılık sayısına eşit olduğunu kanıtlamak için, köklerin katsayıların sürekli fonksiyonları olduğunu bilmek gerekir. Pozitif özellikli cisimler üzerinde deformasyonlar kullanılamaz. Ayrıca, uygun bir deformasyonun tanımlanmasının zor olduğu durumlar (ikiden fazla düzlem eğrinin ortak bir kesişme noktasına sahip olması durumunda olduğu gibi) ve hatta deformasyonun mümkün olmadığı durumlar vardır.[3]
Şu anda, Jean-Pierre Serre'den sonra, katlılık sayısı genellikle katlılık sayısının dikkate alındığı nokta ile ilişkili yerel bir halkanın uzunluğu olarak tanımlanmaktadır. Çoğu spesifik tanım, Serre'nin tanımının özel durumu olarak gösterilebilir.
Bézout teoremi durumunda, teoremin her girdi denklemiyle, bu denklemlerin katsayılarında her çarpanın tek bir kesişme noktasına karşılık geleceği şekilde çarpanlara ayıran bir polinomu ilişkilendiren kanıtlar (aşağıya bakınız) olduğu için, genel kesişim teorisinden kaçınılabilir. Dolayısıyla, bir kesişim noktasının katlılık sayısı, çarpanlara ayırmanın çarpanının katlılık sayısına karşılık gelir. Bu katlılık sayısının deformasyonla elde edilene eşit olduğunun ispatı, kesişme noktalarının sürekli olarak köklere bağlı olmasından kaynaklanmaktadır.
İspatlar
Bileşkeyi (resultant) kullanma (düzlem eğriler)
P ve Q sırasıyla dereceleri p ve q, değişkenleri x, y, t olan iki homojen polinom olsun. Sıfırları, iki izdüşümsel eğrinin homojen koordinatlarıdır. Böylece kesişim noktalarının homojen koordinatları P ve Q'nun ortak sıfırlarıdır.
Birlikte tek bir değişkenin, y olsun, mertebesi toplanarak, katsayıları x ve t türünden homojen polinomlar olan tek değişkenli polinomlar elde edilir.
Teknik nedenlerden ötürü, P ve Q'nun y cinsinden derecelerinin toplam derecelerine (p ve q) eşit olması için koordinatların değiştirilmesi gerekir ve iki kesişme noktasından geçen her doğru (0, 1, 0) noktasından geçmez. (Bu, iki noktanın aynı x Kartezyen koordinatına sahip olmadığı anlamına gelir.)
y değişkenine göre P ve Q'nun ortaya çıkan bileşkesi R(x, t), x ve t türünden aşağıdaki özelliğe sahip homojen bir polinomdur: ile ancak ve ancak P ve Q'nun ortak bir sıfırı olacak şekilde mevcutsa (bkz. Bileşke § Sıfırlar). Yukarıdaki teknik durum şunları sağlar: benzersizdir. Yukarıdaki ilk teknik koşul, bileşkenin tanımında kullanılan derecelerin p ve q olduğu anlamına gelir; bu da R derecesinin pq olduğu anlamına gelir (bkz. Bileşke § Homojenlik).
R, iki değişkenli homojen bir polinom olduğundan, cebirin temel teoremi, R'nin pq doğrusal polinomların bir çarpımı olduğunu işaret eder. P ve Q ortak sıfırının katlılık sayısı, çarpımda karşılık gelen çarpanın tekrar sayısı olarak tanımlanırsa, Bézout'un teoremi böylece kanıtlanmış olur.
Az önce tanımlanan kesişim katlılık sayısının bir deformasyon açısından tanıma eşit olduğunu kanıtlamak için, bileşke ve dolayısıyla doğrusal çarpanlarının P ve Q katsayılarının sürekli fonksiyonları olduğunu belirtmek yeterlidir.
Diğer kesişme katlılık sayısı tanımlarıyla eşitliğin kanıtlanması, bu tanımların teknik özelliklerine dayanır ve bu nedenle bu makalenin kapsamı dışındadır.
U-bileşke'yi kullanma
20. yüzyılın başlarında, Francis Sowerby Macaulay, n değişkenli n homojen polinomun çok değişkenli bileşkesini (Macaulay'ın bileşkesi olarak da bilinir) tanıttı; bu, iki polinomun olağan bileşkesinin genelleştirilmesidir. Macaulay'ın bileşkesi, katsayıları içeren cebirsel kapalı bir cisimde sadece ve sadece polinomların önemsiz olmayan (yani bir bileşeni sıfır olmayan) ortak sıfıra sahip olması durumunda sıfır olan n homojen polinomların katsayılarının bir polinom fonksiyonudur.
U-bileşke, Macaulay tarafından da tanıtılan Macaulay'ın bileşkesinin belirli bir örneğidir. , türünden n + 1 değişkenli n adet homojen polinomu verildiğinde U-bileşke, ve polinomlarının bileşkesidir; burada katsayıları yardımcı değişkenlerdir. U-bileşke, türünden derecesi derecelerinin çarpımı olan homojen bir polinomdur.
Çok değişkenli bir polinom genellikle indirgenemez olsa da, U-bileşke, katsayılarını içeren cebirsel kapalı bir cisim üzerinde doğrusal polinomlar olarak ( şeklinde) çarpanlara ayrılabilir. Bu doğrusal çarpanlar, aşağıdaki şekilde 'nin ortak sıfırlarına karşılık gelir: her ortak sıfıra doğrusal bir çarpan karşılık gelir ve tersi de söylenebilir.
Bu, ortak bir sıfırın katlılık sayısı, U-bileşkeye karşılık gelen doğrusal çarpanının katlılık sayısı olarak tanımlanırsa, Bézout teoremini kanıtlar. Önceki kanıta gelince, bu katlılık sayısının deformasyon yoluyla tanımla eşitliği, U- bileşkenin katsayılarının bir fonksiyonu olarak sürekliliğinden kaynaklanmaktadır.
Bézout'un teoreminin bu kanıtı, modern kesinlik kriterlerini karşılayan en eski kanıt gibi görünüyor.
Bir idealin derecesini kullanmak
Bézout teoremi, aşağıdaki teoremi kullanarak polinomların sayısının tekrarlanmasıyla kanıtlanabilir.
V, boyutu ve derecesinin bir izdüşümsel cebirsel kümesi ve H, herhangi bir indirgenemez V bileşeni içermeyen dereceli bir hiper yüzey (tek bir polinomla tanımlanan) olsun; bu hipotezler altında, V ve H kesişiminin boyutu ve derecesi vardır.
Hilbert dizilerini kullanarak bir (kabataslak) kanıt için, bkz. Hilbert serisi ve Hilbert polinomu § İzdüşümsel bir varyete derecesi ve Bézout teoremi .
Bézout teoreminin kavramsal olarak basit bir ispatına izin vermenin yanı sıra, bu teorem kesişme teorisi için temeldir, çünkü bu teori esasen yukarıdaki teoremin hipotezleri geçerli olmadığında kesişme katlılık sayılarının incelenmesine adanmıştır.
Ayrıca bakınız
- AF+BG teoremi – Diğer iki eğrinin tüm kesişim noktalarından geçen cebirsel eğriler hakkında
- Bernstein–Kushnirenko teoremi – Laurent polinomlarının ortak karmaşık sıfırlarının sayısı hakkında
Notlar
- Dipnotlar
- ^ Bezu diye okunur. Nesin, Ali (2018). Fen Liseleri İçin Matematik 3-Tamsayılar Yapısı. s. 53. ISBN 9786059569187.
- Notlar
- ^ O'Connor, John J.; Robertson, Edmund F., "Bézout teoremi", MacTutor Matematik Tarihi arşivi
- ^ Kirwan, Frances Clare (1992). Complex Algebraic Curves. United Kingdom: Cambridge University Press. ISBN 0-521-42353-8.
- ^ Kerner, D. (2008), On the δ= const Collisions of Singularities of Complex Plane Curves, s. 5
Konuyla ilgili yayınlar
- Bezout’s Theorem (PDF), 4 Eylül 2019 tarihinde kaynağından (PDF) arşivlendi,
Kitap bölümü
- Toni Annala, Bézout's theorem (PDF), 7 Mayıs 2021 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 14 Ekim 2020
- Introduction to Algebraic Geometry - Bézout’s Theorem and Inflection Points (PDF), 30 Mart 2007 tarihinde kaynağından (PDF) arşivlendi
- Andreas Gathmann, Applications of Bézout’s Theorem (PDF), 16 Ekim 2020 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 14 Ekim 2020,
Kitap bölümü
Dış bağlantılar
- Hazewinkel, Michiel, (Ed.) (2001), "Bezout theorem", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Eric W. Weisstein, Bézout's Theorem (MathWorld)
- "Bezout's Theorem", MathPages, 31 Ocak 2020 tarihinde kaynağından arşivlendi
- YouTube'da Bezout's Theorem (Video, 15:02 dk)
Kaynaklar
- Fulton, William; Weiss, Richard (1974). Algebraic Curves: An Introduction to Algebraic Geometry. Mathematics Lecture Note Series. W.A. Benjamin. s. 112. ISBN 978-0805330823.
- Newton (1966). Principia Vol. I The Motion of Bodies. based on Newton's 2nd edition (1713); translated by Andrew Motte (1729) and revised by Florian Cajori (1934). Berkeley, CA: University of California Press. ISBN 978-0-520-00928-8. Newton Principia’nın önceki (2.) baskısının alternatif çevirisi.
- generalization of Bezout's Theorem?, erişim tarihi: 10 Mart 2021,
(Teoremin genelleştirilmesi)
















































